Bead model reconstructions
This tutorial covers basic principles and best practices for creating bead (dummy atom) model reconstructions of macromolecule shape from SAXS data. This is not a tutorial on how to use RAW for this type of analysis. For that, please see the RAW tutorial for DAMMIF/N.
Overview
A natural desired outcome for many SAXS experiments is determining the ‘solution structure’ of the sample, i.e. the structure of the macromolecule as it exists in solution. Unfortunately, unlike crystallography, cryoEM, and NMR, SAXS data cannot be used to generate a high resolution 3D shape (though it can be used to constrain other methods of structure determination). What SAXS can often provide, and what is a common end point of SAXS analysis, is a low resolution shape reconstruction of the sample.
For many years, bead modeling was the state of the art approach for generating these low resolution shape reconstructions. Recently, other techniques have been developed, such as direct reconstruction of the electron density at low resolutions. Despite this, bead modeling remains the de facto standard for shape reconstruction.
Why do we do bead model reconstructions?
Bead models, despite their low resolution, can be powerful tools for understanding the system in solution. High resolution structures can be docked into the bead model, allowing visual analysis of how well the high resolution structure agrees with the solution structure. In the absence of other structure information, bead models can be used to provide important clues to the overall shape and size of the system, which can often be enough to draw conclusions about important aspects of the macromolecular function or interactions with other systems.
While bead modeling can be quite useful, it is important to always keep in mind two things. First, it is very easy to get poor reconstructions, even with good quality data, and you must carefully evaluate the results of your reconstructions before using them. Second, SAXS is much more accurate at hypothesis testing than it is at generating bead models. Put another way SAXS is very good at telling you what something isn’t, but not so good at telling you what it is. For example, if you want to compare a high resolution structure to SAXS data and see if they agree, you are always better off testing the calculated scattering profile of the high resolution structure against the measured scattering profile than docking the structure into the bead model. In this case, the bead model might be useful in visualizing the differences between the solution shape and your high resolution structure.
How do we do bead model reconstructions?
There are a number of different programs available to do bead modeling, some suited for general systems and some tuned for very specific applications like reconstructions of membrane proteins with detergent halos. Regardless, all of these methods share a similar approach.
Generate a volume of beads (aka ‘dummy atoms’) and randomly assign the beads to be one of the allowed phases. In general, beads are either solvent or macromolecule, but some programs allow more than 2 phases, such as differentiating between protein and RNA or macromolecule and lipid.
Calculate a scattering profile from the bead model and fit that against the data.
Flip a randomly chosen set of beads between phases (e.g. from solvent to macromolecule or vice versa).
Recalculate the scattering profile from the model and the to the data.
If the fit is better, accept the changes to the beads. If the fit is worse, accept the changes to the beads with some probability (avoids local minima).
Repeat steps 3-5 until the convergence criteria is met.
Additional, programs usually impose physical constraints on the bead models to improve the model. Common constraints are requiring connectivity of the model, imposing penalties for extended models, and constraining the size of the model based on the Rg and/or Dmax.
It turns out that a scattering profile does not generate a unique reconstruction, so to account for this a Monte Carlo like approach is taken where a number (usually 10-20) of models are generated, and then averaged to give a consensus reconstruction.
The most common program for creating bead model reconstructions (though far from the only such program) is DAMMIF (or DAMMIN) [1-2] from the ATSAS package. For the remainder of this tutorial we will exclusively discuss using DAMMIF/N, though much of the discussion should apply to other programs as well.
Using DAMMIF/N for bead model reconstructions
DAMMIF is the most commonly used program for bead model reconstructions. Here we discuss some of the practical aspects. A detailed tutorial of how to use DAMMIF in RAW is also available.
Input data
DAMMIF requires a P(r) function generated by GNOM (a .out file) as input. Note that, as mentioned in the IFT tutorial, the scattering profile for the IFT should be truncated to a maximum q value of 8/Rg or ~0.25-0.30 1/Angstrom, whichever is smaller. This is because the hydration layer and internal structure are not modeled by DAMMIF, which leads to errors at higher q. The truncation removes the potentially problematic higher q data.
Generating models
As bead modeling does not generate a unique solution. In order to generate a reasonable solution, we create 10-20 bead model reconstructions and then average them. I recommend 15 reconstructions. This means that we need to run DAMMIF 15 different times.
The most accessible settings for DAMMIF are the Mode, Symmetry, and Anisometry.
Mode: For mode, options are Fast or Slow. Fast is quick, but less detailed, Slow is the opposite. For a final reconstruction, use Slow mode.
Symmetry: Adding in symmetry constraints can improve the reconstruction. If you know the symmetry of the particle, you can specify this. However, it is always recommend that you do an additional set of reconstructions with P1 symmetry, to verify that the symmetry did not overly constrain the reconstructions.
Anisometry: Adding in anisometry constraints can improve the reconstruction. If you know the anisometry of the particle, you can specify this. However, it is always recommend that you do an additional set of reconstructions with no anisometry, to verify that the symmetry did not overly constrain the reconstructions.
Additional advanced options are available, and are described in the DAMMIF manual.
If you only want a quick look at the shape (such as when collecting data at a beamline) 3 reconstructions in Fast mode will work for that purpose.
Averaging and clustering models
After models are generated the next step is to average and cluster the models. Averaging generates a consensus shape from the individual models, and provides statistics on how stable the reconstruction is. This is done with DAMAVER [3]. The average outputs both damaver.pdb and damfilt.pdb model files. These correspond to two different consensus shapes of the model, loosely and tightly defined respectively. However, neither of these models actually fits the data, and so generally should not be used to display your reconstructions. DAMAVER will also specify the most probably individual model. If you do not refine the results of DAMAVER (below) you should use the most probable model as your final result.
Clustering is done with DAMCLUST [4] and clusters models that are more similar to each other than they are to the rest of the models. This is a way of assessing the ambiguity of the reconstruction, and we will discuss it further in the section on evaluating reconstructions below.
Creating a final refined model
The output of DAMAVER, specifically the damstart.pdb file, can be used as input for DAMMIN to create a final refined model. Essentially, the damstart.pdb represents a conservative core of the most probably occupied volume as determined by averaging all the reconstructions using DAMAVER. DAMMIN keeps this core fixed, and refines the outside of the model to match the scattering profile. I’ve seen mixed recommendations (even from the makers of the software) on whether you should do a refinement. I typically do, but it seems you can often do just as well with the most probable model determined by DAMAVER.
Evaluating DAMMIF/N reconstructions
SAXS data contains very limited information, both because it is measured at relatively low q, and because it is measured from a large number of particles in solution oriented at random angles. The SAXS scattering profile represents the scattering from a single particle, averaged over all possible orientations. The practical consequence of this is that there are often several possible shapes that could generate the same (or so similar as to be indistinguishable within experimental noise) scattering profiles. As such, it may simply not be possible to generate a bead model reconstruction from a dataset that accurately represents the solution shape, regardless of the overall data quality. If the sample is flexible or otherwise exists in multiple conformational or oligomeric states in solution the reconstruction is also challenging or impossible. In summary, high quality SAXS data is not a guarantee of a good bead model reconstruction. This makes it very important to critically evaluate every reconstruction done, regardless of the underlying data quality.
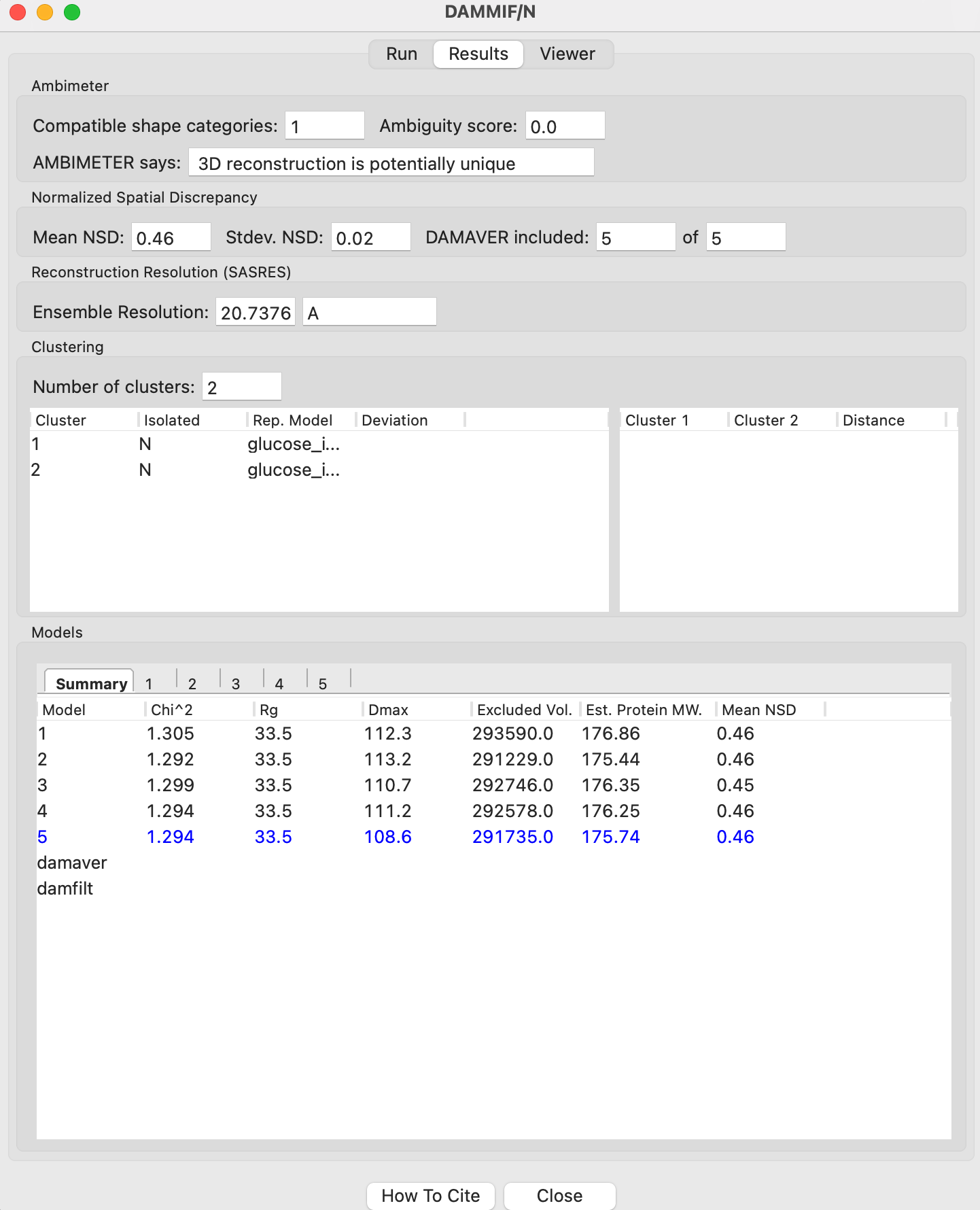
The information needed to evaluate the reconstructions is generated when running DAMMIF, DAMAVER, DAMCLUST, SASRES [5] (run as part of DAMAVER) and AMBIMETER [6]. While it can all be accessed through the files these programs generate, RAW gathers and presents it for you when you run DAMMIF in RAW.
Criteria for a good DAMMIF/N reconstruction
Ambiguity score < 2.5 (preferably < 1.5)
NSD < 1.0
Few (0-2) models rejected from the average
Only one cluster of models
Model \(\chi^2\) near 1.0 for all models
Model Rg and Dmax close to values from P(r) function for all models
M.W. estimated from model volume close to expected M.W.
More about these criteria can be found below.
Ambiguity
It is possible to evaluate the potential ambiguity of your bead model reconstructions before doing the reconstructions. The AMBIMETER program in the ATSAS package can be run on P(r) functions from GNOM to assess how likely you are to get a good reconstruction. The program has a database of scattering profiles representing all possible shapes made out of up to 7 beads. Your scattering profile is compared against these shapes, and AMBIMETER reports how many match your profile. The more profiles from AMBIMETER that match yours, the more possible shapes could have generated your profile.
AMBIMETER reports both the number of shapes and the log (base 10) of the number shapes, which is the Ambiguity score. They provide the following interpretations:
Ambiguity score < 1.5 - Reconstruction is likely unique
Ambiguity score of 1.5-2.5 - Take care when doing the reconstruction
Ambiguity score > 2.5 - Reconstruction is most likely ambiguous.
This provides a quick initial assessment of whether you should even attempt a shape reconstruction for your dataset. You can run AMBIMETER from RAW.
Normalized spatial discrepancy
DAMAVER reports a number of different results. The most useful is the normalized spatial discrepancy (NSD). This is essentially a size normalized metric for comparing how similar two different models are. When DAMAVER is run, it reports the average and standard deviation of the NSD between all the reconstructions. It also reports the average NSD for each model.
The average NSD is commonly used to evaluate the stability of the reconstruction. Roughly speaking we evaluate reconstruction stability as:
NSD < 0.6 - Good stability of reconstructions
NSD between 0.6 and 1.0 - Fair stability of reconstructions
NSD > 1.0 - Poor stability of reconstructions
Generally speaking, if your average NSD is less than 1.0, the reconstruction can probably be trusted (if all of the other validation metrics also check out), while if it is greater than 1.0 you should proceed with caution, or not use the reconstructions at all.
The NSD is also used to determine which models to include in the average. If the average NSD of a given model is more than two standard deviations above the overall average NSD, that model is not included in the average. If more than ~2 models are rejected (out of 15), that may be a sign of an unstable reconstruction.
Clusters
DAMCLUST creates clusters of models that are more similar to each other than they are to the rest of the models. This is a way of assessing the ambiguity of the reconstruction. If you have more than one cluster of models in your reconstructions, you may have several distinct shapes that are being reconstructed by the DAMMIF algorithm. This typically indicates that there are several distinct shapes in solution that could generate the measured scattering profile, and so is another indication of a highly ambiguous reconstruction.
The caveat to this is that with good quality data that is very low ambiguity (ambiguity score from AMBIMETER < 0.5) and yields a set of reconstructions with a very small average NSD (<0.5, typically) and NSD standard deviation (~0.01), I have seen several (often >5) clusters identified with DAMCLUST. I believe that in this case there are not actually multiple clusters, but the extremely low deviation between the models is fooling the DAMCLUST algorithm.
Note that the different clusters should not be taken as representatives of different distinct shapes in solution. Even if there are a finite number of distinct shapes scattering in the solution (such as an open and closed state of a protein), the measured scattering profile is an average of the scattering from each component, and each individual reconstruction fits that measured scattering profile. As such, there is no way for an individual reconstruction to fit just the scattering from one of the components and so the different clusters cannot be representative of the different shapes in the solution.
Model fit and parameters
Each model has the following parameters that can be used to evaluate the success of an individual reconstruction: \(\chi^2\), Rg, Dmax, volume, molecular weight estimated from volume, and the normalized residual of the model fit to the data. For a good fit to the data, the model \(\chi^2\) should be close to 1 and the normalized residual between the model fit and the data should be flat and randomly distributed about zero. However, in my experience the normalized residual often shows some small systematic deviations, and so this should not be too concerning. A \(\chi^2\) value significantly larger than 1 (1.5-2 or larger) indicates either a poor fit to the data or that the uncertainty for the data is underestimated. To differentiate between these two cases, look at the normalized residual. If it is flat and randomly distributed, then the uncertainty is most likely underestimated. If it shows significant systematic deviations then the fit quality is poor.
The Rg and Dmax obtained from the model should be close to those calculated from the P(r) function. If that is not the case, you should reevaluate your P(r) function and redo the reconstruction if necessary. If the discrepancy persists, it is an indication that your reconstruction isn’t a good representation of what is in solution, and shouldn’t be trusted. While there’s no hard and fast rule here on how closely Rg and Dmax should agree, my experience is generally that for high quality data Rg agrees to better than ~5% and Dmax to ~10%.
The volume is reported for each bead model, but it is usually easier to compare the molecular weight calculated from that volume with the expected molecular weight. In this case, M.W. is calculated by dividing the volume (nominally representing the sample’s excluded volume) by an empirically determined constant [4] of 1.66 (used in RAW, other programs may use different values). This value is approximate, and varies between roughly 1.5 and 2.0 depending on the shape of the macromolecule. This M.W. is less well determined than other SAXS methods, given the variation in the coefficient. As such, it is mostly useful for indicating general agreement between the overall size of the reconstruction and the expected size. If the M.W. is different from the expected M.W. by more than 20-25% you should consider the reconstructions to be suspect.
Limitations of bead models
While bead models can be quite useful, they have a number of limitations, many of which are mentioned in previous parts of the tutorial. In summary:
Bead models can be ambiguous, even if the data quality is very high. This is because multiple different shapes in solution can produce the same scattering profile, so there is no guaranteed unique solution to a reconstruction, and the success of the reconstruction depends not just on the input data quality but also the inherent shape of the particle and how ambiguous that shape is for SAXS. Because of this, all models should be thoroughly evaluated as described above.
Ignoring ambiguity, bead models still only work best with particular particle shapes. An excellent discussion of how well bead models work for different types of shapes is found in [3]. The summary is that bead models tend to be less reliable for high aspect ratio objects, such as long rods or thin discs, objects with voids (such as a spherical shell), and rings. They are most reliable for things that are generally globular.
Bead models are low resolution. Small variations of the surface of the model are likely insignificant. I rarely see estimated model resolutions less than ~20 Angstroms, often they are much larger.
Bead models do not (typically) model the hydration layer or internal structure of the particle. This requires that you use only data out to a maximum q of 8/Rg or ~0.25-0.30 1/Angstrom, whichever is less.
The most common bead modeling programs cannot model multiple electron densities within a sample, such a protein-nucleic acid complex or a membrane protein with a detergent halo. There are specialized programs (such as MONSA or Memprot) that can handle these cases, but these require the input of additional information to provide extra constraints.
The bead model is only as good as the input data. In particular, bead models are quite sensitive to the presence of larger particles in solution, either oligomers or non-specific aggregate. In one simple simulation I’ve seen, as little as 0.7% aggregate caused a significant change in the bead model. Non-specific aggregation usually manifests as an extended protrusion from the main model.
As you can see, while bead models can certainly be useful for your research, you should proceed with caution and ensure that you have a trustworthy reconstruction before proceeding with your bead models.
Visualizing DAMMIF/N reconstructions
Visualizing DAMMIF/N bead model reconstruction is slightly different from displaying a typical macromolecular structure. There are two main ways that these are visualized, either as individual beads or, more commonly, as an envelope that defines the edges of the model. Both representations are usually made semi-transparent so that a high resolution structure docked with the bead model is simultaneously visible.
The main detail to remember is that to get a correct visualization you have to set the correct bead size for the model, which is given in the header of the DAMMIF/N .cif file.
Below are two quick tutorials for visualizing models in Chimera (or ChimeraX) and PyMOL.
Visualizing bead models with Chimera
Note: There are some differences between Chimera and the newer ChimeraX. Differences for ChimeraX are noted in bold.
Open Chimera.
Load in the DAMMIF/N .cif file of interest.
If necessary, open the Model Panel and the Command Line from the Tools-> General Controls menu.
In the Select->Chain menu choose the bead model (“no ID” or the filename).
In the Actions->Ribbons (Actions->Cartoon) menu, choose “Hide”.
In the Actions->Atoms/Bonds menu, choose “Show”.
In the Actions->Atoms/Bonds (Actions->Atoms/Bonds->Atom Style) menu choose “Sphere”.
In the Camera section of the ChimeraX “Graphics” ribbon, click “View selected”.
Open the .cif file in a text editor.
Find the “Dummy atom radius” value. That is the bead size you need to set.
In the command line, enter the command
vdwdefine x #ywherexis the bead size from the PDB header andyis the ID number of the bead model shown in the model panel.The command is “size atomradius x” in ChimeraX.
Your beads are now the right size. If you want to make an envelope proceed with the following optional steps. If you’d rather use the individual bead display, you can stop here.
To make an envelope, in the command line enter the command
molmap #y zwhereyis the ID number of the bead model shown in the model panel andzis 3x the bead size that you found in the previous steps.Tip: The last number controls the smoothness of the envelope. You may need to vary it from 3*(bead size), depending on the size of your beads and how smooth you want your envelope. I recommend leaving at least a hint of the beads visible (not overly smoothing the envelope) to help whoever sees the graphic to remember that an envelope is not an electron density contour.
Hide the bead model using the “Hide” button in the model panel.
In the Volume Viewer window that appeared when you entered the molmap command, in the Features menu select the “Surface and Mesh options’.
Note: This menu doesn’t exist in ChimeraX.
Check the box for Surface smoothing and set the iterations to 2 and the factor to 1.
Note: This option doesn’t exist in ChimeraX.
Check the box for Subdivide surface and set it to 2 times.
Note: This option doesn’t exist in ChimeraX.
Click on the color box to set color and opacity. I find that 0.4 (40%) is a good opacity for overlaying with high resolution models.
Load in your aligned (such as with SUPCOMB) high resolution structure if available.
Visualizing bead models with PyMOL
Open PyMOL
Load in the DAMMIF/N .cif file of interest.
Using the model Hide menu (‘H’), hide ‘everything’.
Using the model Show menu (‘S’), show ‘spheres’.
Open the .cif file in a text editor and find the “Dummy atom radius” value in the header.
In the PyMOL command line, enter the command
alter <model_name>, vdw=xwherexis the size you found in the previous step. This sets the spheres to be the correct size of the beads in the model.Click the ‘Rebuild’ button to refresh the view of the model.
Your model is now displayed correctly with beads. If you want to make an envelope, proceed with the following optional steps. If you’d rather use the individual bead display, you can stop here.
Using the model Show menu, show ‘surface’.
Using the model Hide menu, hide ‘spheres’.
You can smooth the surface by increasing the probe radius using the command
set solvent_radius, 3.0(where you can vary the size from 3.0).You can improve the quality of the surface using the command
set surface_quality, 1.Note: Values larger than 1 may take a long time to render.
Set your surface transparency to 50% for overlaying with high resolution models using the command
set transparency, 0.5Load in your aligned (such as with SUPCOMB) high resolution structure if available.
FAQ
Do I have to make a bead model?
No. It all depends on what you’re trying to say about the data. However, particularly if your system shows signs of flexibility or AMBIMETER reports a high ambiguity score you probably shouldn’t bother making a bead model even if you want to.
How do I fit my high resolution structure into my bead model?
If your high resolution structure is relatively complete (contains all residues in solution, and ideally post-translational modifications), you can use a program like SUPCOMB [7] to automatically fit the structure into the bead model. If you are missing significant amounts of the structure (such as a large flexible loop) or have only one subunit of a multi-subunit complex you may have to manually dock the structure in the envelope.
My bead model and my high resolution structure disagree. Which one is right?
Maybe both, maybe neither! It really depends on your inputs. If you’ve validated the bead model as above and it seems good, then it likely represents the low resolution shape in solution. You should also verify that your high resolution shape contains all of the residues in your system, often high resolution structures are missing things like flexible loops or N and C terminus regions.
If both models are good, then depending on how you obtained your high resolution shape it might also be correct, but represent the shape under different conditions. For example, it is common in crystallography to see structural artifacts induced by the packing of the macromolecule into the crystal.
Of course, the best way to compare your high resolution structure to SAXS data isn’t by docking it in a bead model, but by fitting it against the data using a program like CRYSOL or FoXS. If these fits are bad, then your high resolution structure doesn’t match the data, regardless of what the bead model shows. If these fits are good, and the bead model doesn’t agree with the high resolution structure, then the bead model is wrong.
My bead model isn’t good, what should I do instead?
There are many more approaches available than I can list here, but a couple of the more common ones are:
References
Franke, D. and Svergun, D.I. (2009) DAMMIF, a program for rapid ab-initio shape determination in small-angle scattering. J. Appl. Cryst., 42, 342-346.
D. I. Svergun (1999) Restoring low resolution structure of biological macromolecules from solution scattering using simulated annealing. Biophys J. 2879-2886.
V. V. Volkov and D. I. Svergun (2003). Uniqueness of ab-initio shape determination in small-angle scattering. J. Appl. Cryst. 36, 860-864.
Petoukhov, M.V., Franke, D., Shkumatov, A.V., Tria, G., Kikhney, A.G., Gajda, M., Gorba, C., Mertens, H.D.T., Konarev, P.V. and Svergun, D.I. (2012) New developments in the ATSAS program package for small-angle scattering data analysis. J. Appl. Cryst. 45, 342-350
Anne T. Tuukkanen, Gerard J. Kleywegt and Dmitri I. Svergun(2016) Resolution of ab initio shapes determined from small-angle scattering IUCrJ. 3, 440-447.
M.V. Petoukhov and D.I. Svergun (2015) Ambiguity assessment of small-angle scattering curves from monodisperse systems Acta Cryst. D71, 1051-1058.
M.Kozin & D.Svergun (2001) Automated matching of high- and low-resolution structural models J Appl Cryst. 34, 33-41.