Advanced Series processing – Regularized Alternating Least Squares (REGALS)
REGALS is an algorithm for deconvolution of mixtures in small angle scattering data. It can be applied to deconvolving overlapping peaks in SEC-SAXS, changing baseline and elution peaks in ion exchange chromatography SAXS, mixtures in time resolved SAXS data and equilibrium titration series data, and likely other cases. In practical application it can be thought of as an extension of the evolving factor analysis (EFA) technique to more complex conditions where components are not necessarily entering and exiting the dataset in a strict first-in-first-out approach like in SEC-SAXS. EFA is recommended for standard SEC-SAXS data, but for more complex data, as listed above, you should use REGALS. REGALS can also handle deconvolution of SEC-SAXS data with a sloping baseline.
To learn more about REGALS we recommend these resources:
REGALS: a general method to deconvolve X-ray scattering data from evolving mixtures S. P. Meisburger, D. Xu, and N. Ando. IUCrJ (2021). 8(2), 225-237. DOI: 10.1107/S2052252521000555
If you use REGALS in RAW, in addition to citing the RAW paper, please cite the REGALS paper: S. P. Meisburger, D. Xu, and N. Ando. IUCrJ (2021). 8(2), 225-237. DOI: 10.1107/S2052252521000555
The written version of the tutorial follows.
Deconvolving ion exchange chromatograph coupled SAXS (IEC-SAXS) data
Ion exchange chromatography is similar to size exclusion chromatography, except that it uses a charged column media and a salt gradient to separate samples by charge rather than size. IEC-SAXS (sometimes called anion exchange or AEX-SAXS) can be useful in cases where there are multiple species in solution that are not separable by size. However, the use of a salt gradient causes a changing buffer background for the sample, making accurate buffer subtraction challenging. REGALS can be used to deconvolve the scattering of the eluted macromolecules from the changing scattering of the buffer.
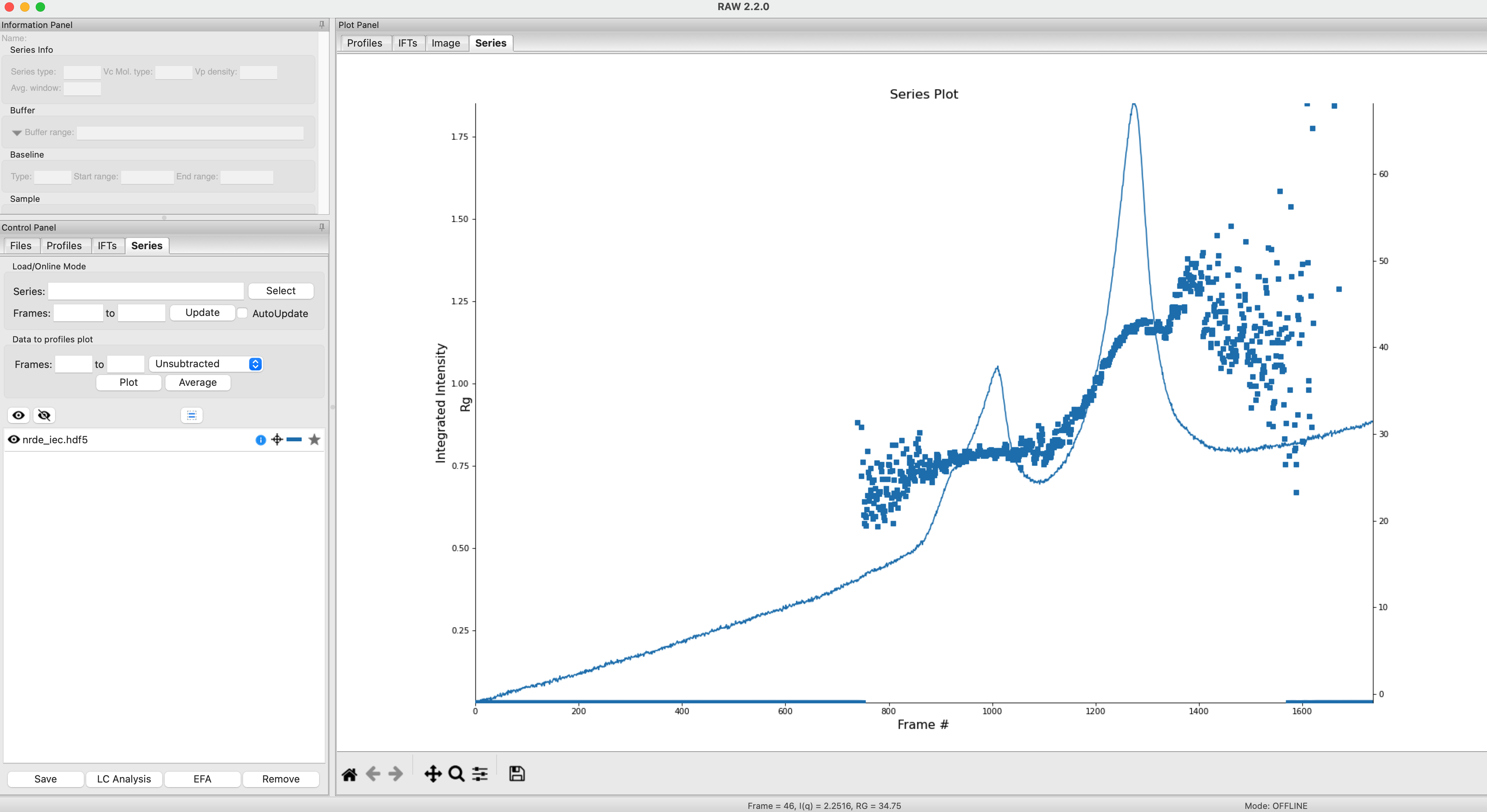
Clear all of the data in RAW. Load the nrde_iec.hdf5 file in the series_data folder.
Note: The data were provided by the Ando group at Cornell University, and were originally published in the paper: Parker, M. J. et al. (2018). An endogenous dAMP ligand in Bacillus subtilis class Ib RNR promotes assembly of a noncanonical dimer for regulation by dATP. Proc Natl Acad Sci USA 115, E4594–E4603. DOI: 10.1073/pnas.1800356115. It is also available from the REGALS github repository.
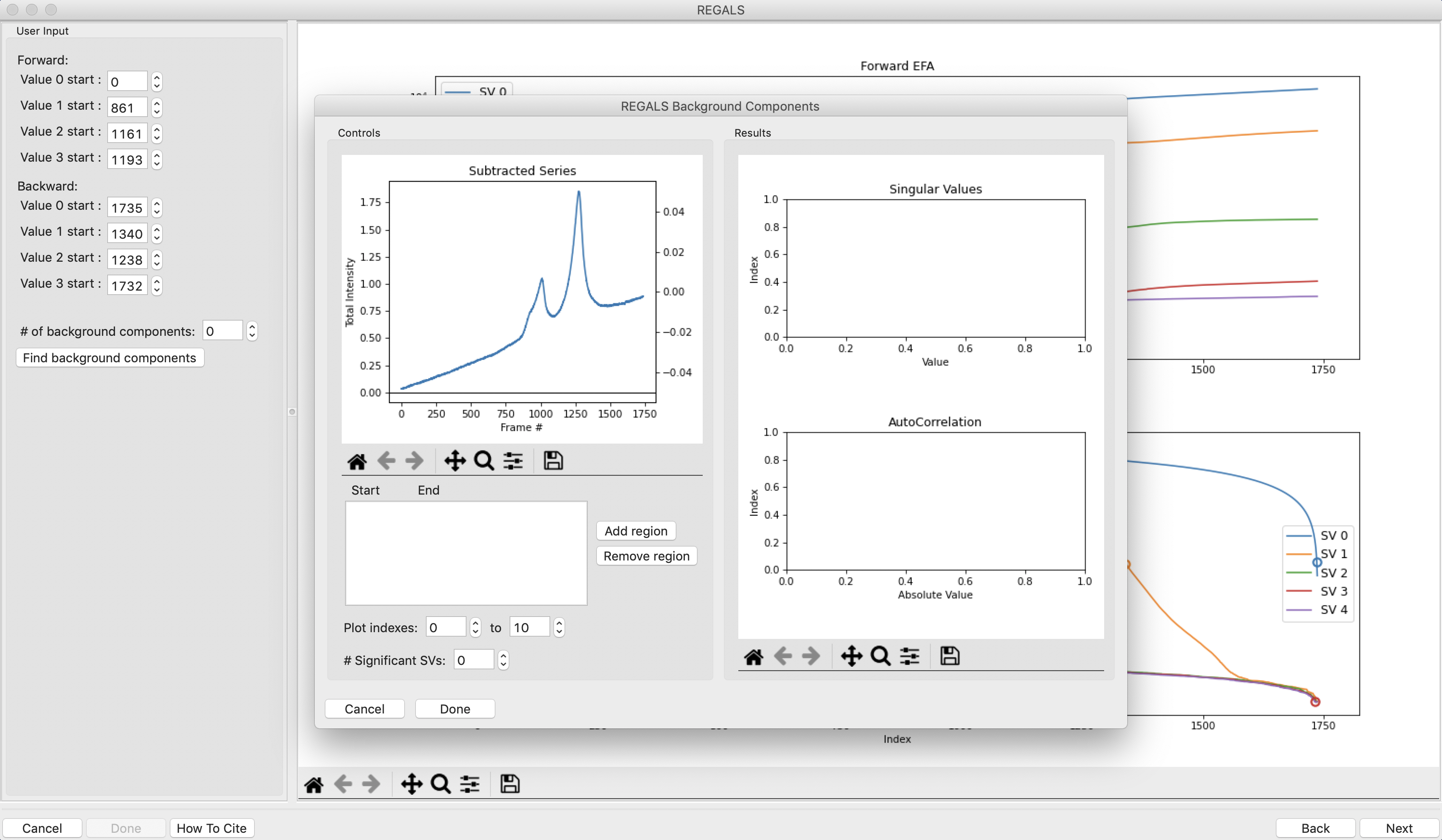
We will use REGALS to extract out the scattering components in both peaks of the data. Right click on the nrde_iec.hdf5 item in the Series list. Select the “REGALS” option.
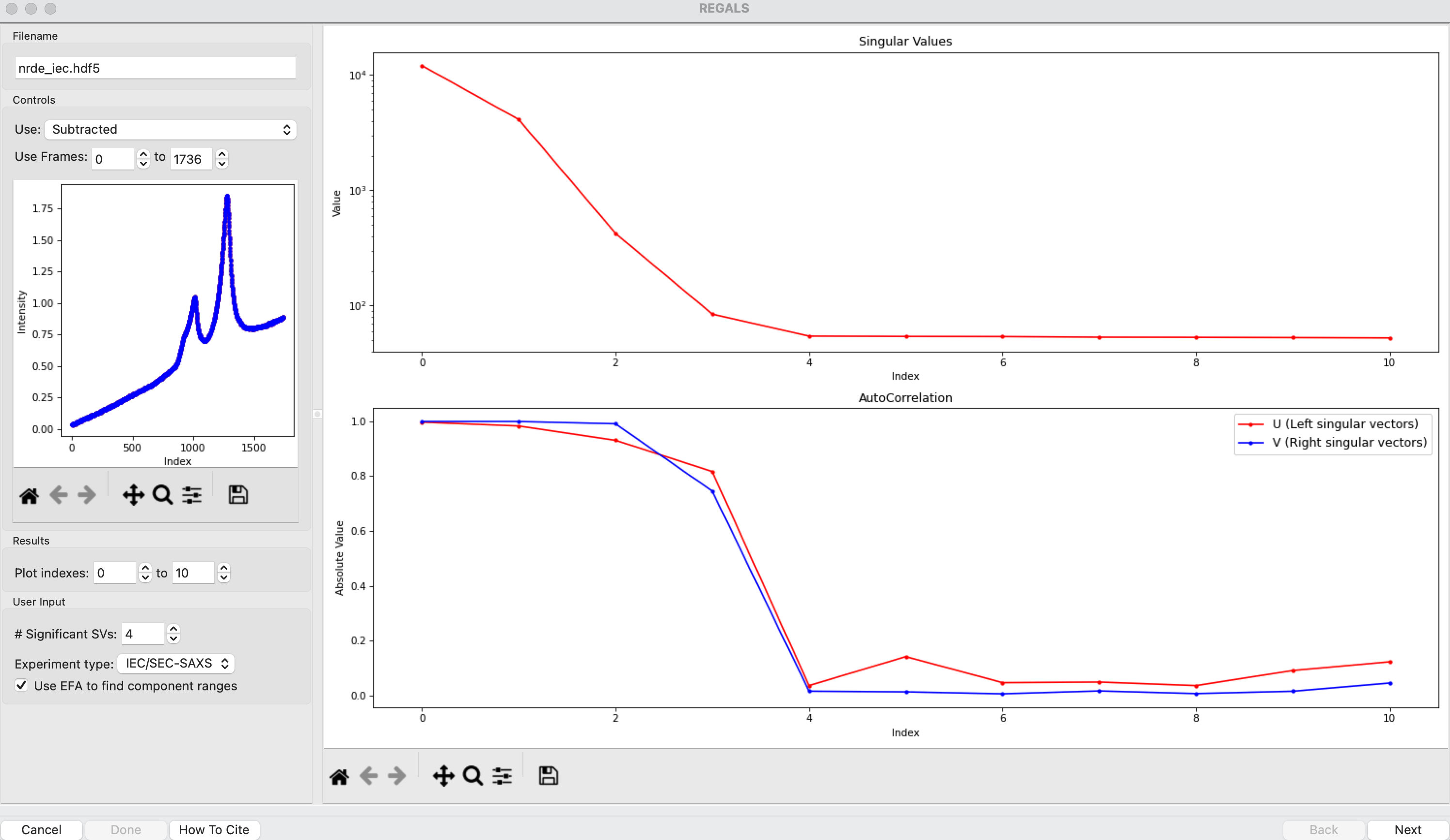
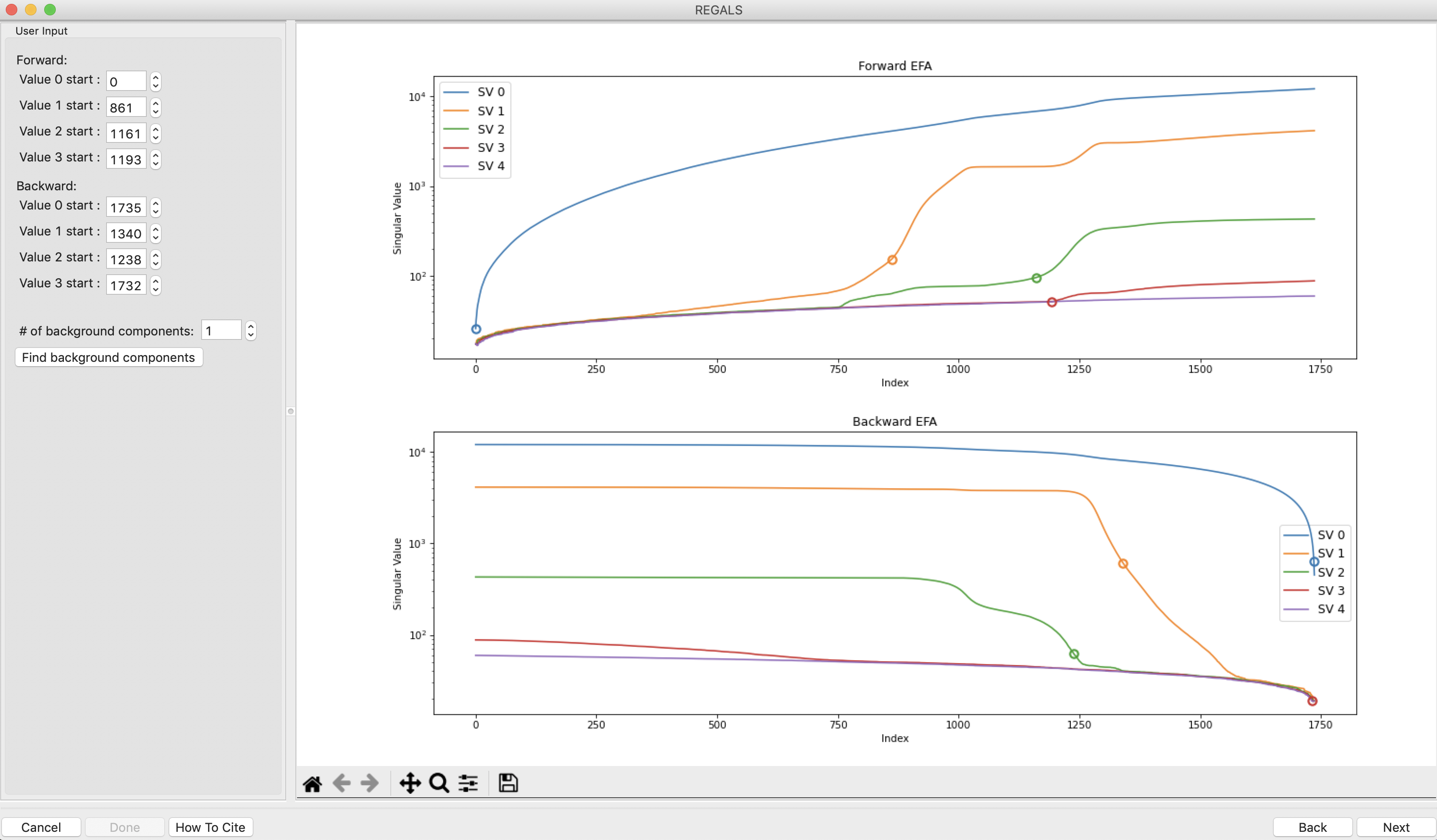
The REGALS window will be displayed. On the left are controls, on the right are plots of the value of the singular values and the first autocorrelation of the left and right singular vectors.
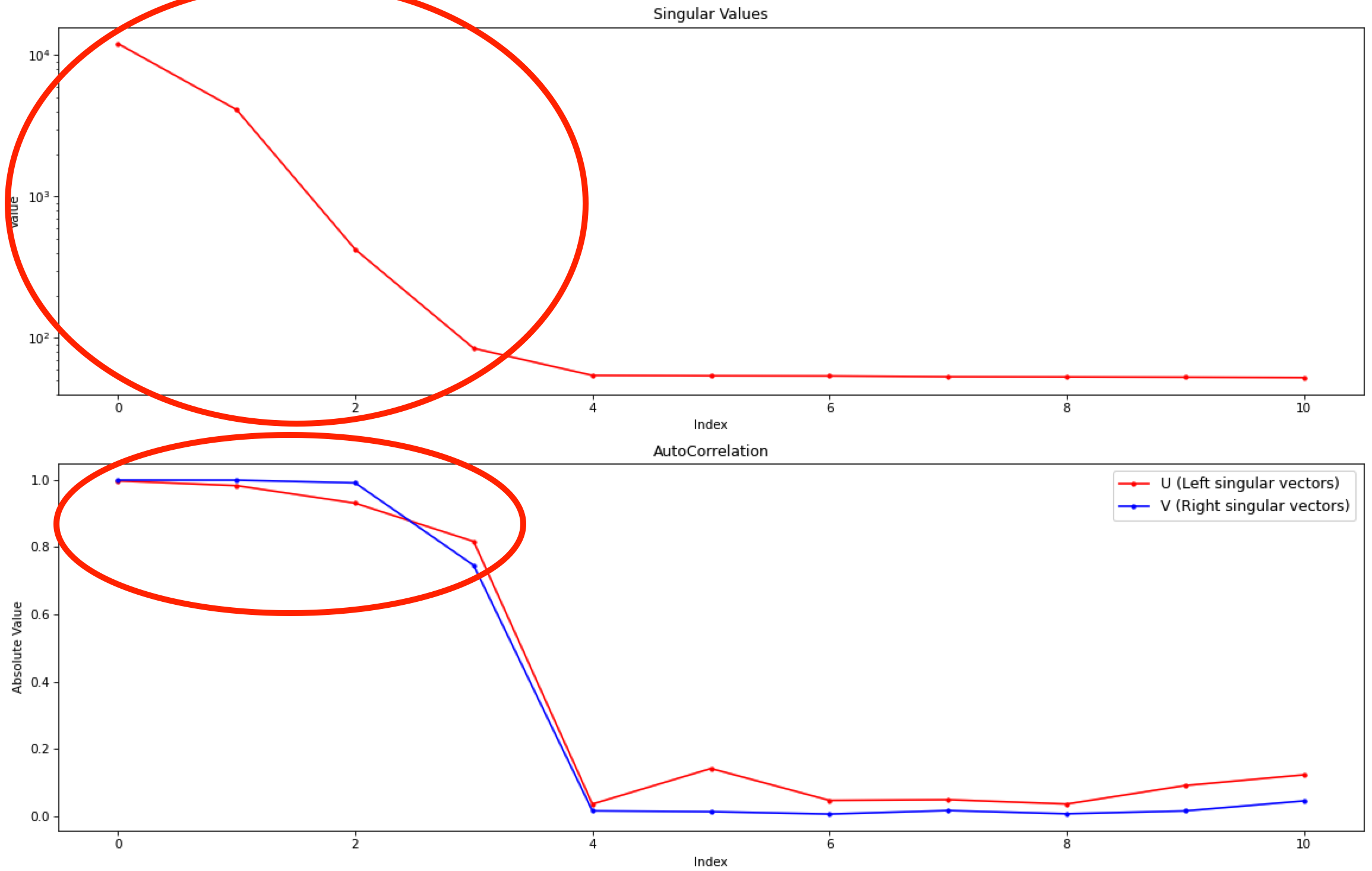
Note: Large singular values indicate significant components. What matters is the relative magnitude, that is, whether the value is large relative to the mostly flat/unchanging value of high index singular values.
Note: A large autocorrelation indicates that the singular vector is varying smoothly, while a low autocorrelation indicates the vector is very noisy. Vectors corresponding to significant components will tend to have autocorrelations near 1 (roughly, >0.6-0.7) and vectors corresponding to insignificant components will tend to have autocorrelations near 0.
Nominally REGALS should work with either subtracted or unsubtracted data. Here, a buffer measured before the start of the dataset has been subtracted off of all the profiles in the dataset. This helps reduce the magnitude of the buffer components in the data, which can make it easier to refine the macromolecular components. We will use the full range of the dataset, but REGALS can also be done on restricted ranges.
Note: Using a restricted range for REGALS might be useful to exclude one or more components of a complicated elution from the deconvolution. The more components you have the harder it is to do REGALS. There is a trade off in the amount of data used (more is better) and the number of components in the deconvolution (fewer is better) that can require some experimentation to find the right balance for a given dataset.
RAW attempts to automatically determine how many significant singular values (SVs) there are in the selected range. This corresponds to the number of significant scattering components in solution that REGALS will attempt to deconvolve. At the bottom of the control panel, you should see that RAW thinks there are four significant SVs (scattering components) in our data. For this data set, that is accurate. We evaluate the number of significant components by how many singular values are above the baseline, and how many components have both left and right singular vectors with autocorrelations near one. For this data there are four singular values above baseline, and four singular vectors with autocorrelations near 1 (see step 3).
Note: Typically you expect the number of significant singular values and the number of singular vectors with autocorrelations near 1 to be equal. If they aren’t, it likely indicates a weak or otherwise poorly resolved component in the dataset. Try the deconvolution first with the lower then the higher number of components.
Note: RAW can find the wrong number of components automatically. You will always want to double check this automatic determination against the SVD results in the plots. If you change the data range used (or data type), the number of components will not automatically update so you should check and update it if necessary.
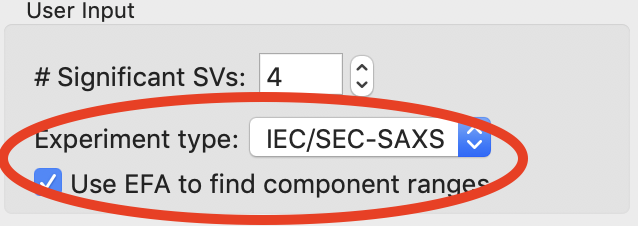
For REGALS there are two other settings you should check. First, set the experiment type. In this case, the default of ‘IEC/SEC-SAXS’ is correct. This sets default values later on in the deconvolution. Second specify whether you want to use the evolving factor plots to find initial guesses for the range of components in solution. This is useful in highly sampled datasets like IEC-SAXS, but may not be very accurate for more sparsely sampled data like a titration series, and so can be skipped. For this dataset leave it checked.
Click the “Next” button in the lower right-hand corner of the window to advance to the second stage of the REGALS analysis
Note: If, as in this case, you are going to use the EFA plots to find the component ranges, it will take some time to compute the necessary values for this next step, so be patient.
A new window will open on top of the current one when you click “Next”. The bottom window is the main REGALS window, with the forward and backward evolving factor plots. On top of that is the REGALS Background Components window. We will first use the Background Components window to estimate how many of our components are background components.
Note: For the purposes of REGALS, a background component is a component that spans the full range of the dataset.
Note: If you select an experiment mode other than ‘IEC/SEC-SAXS’ the Background Components window will not open automatically, but can still be opened by clicking the “Find background components” button if desired.
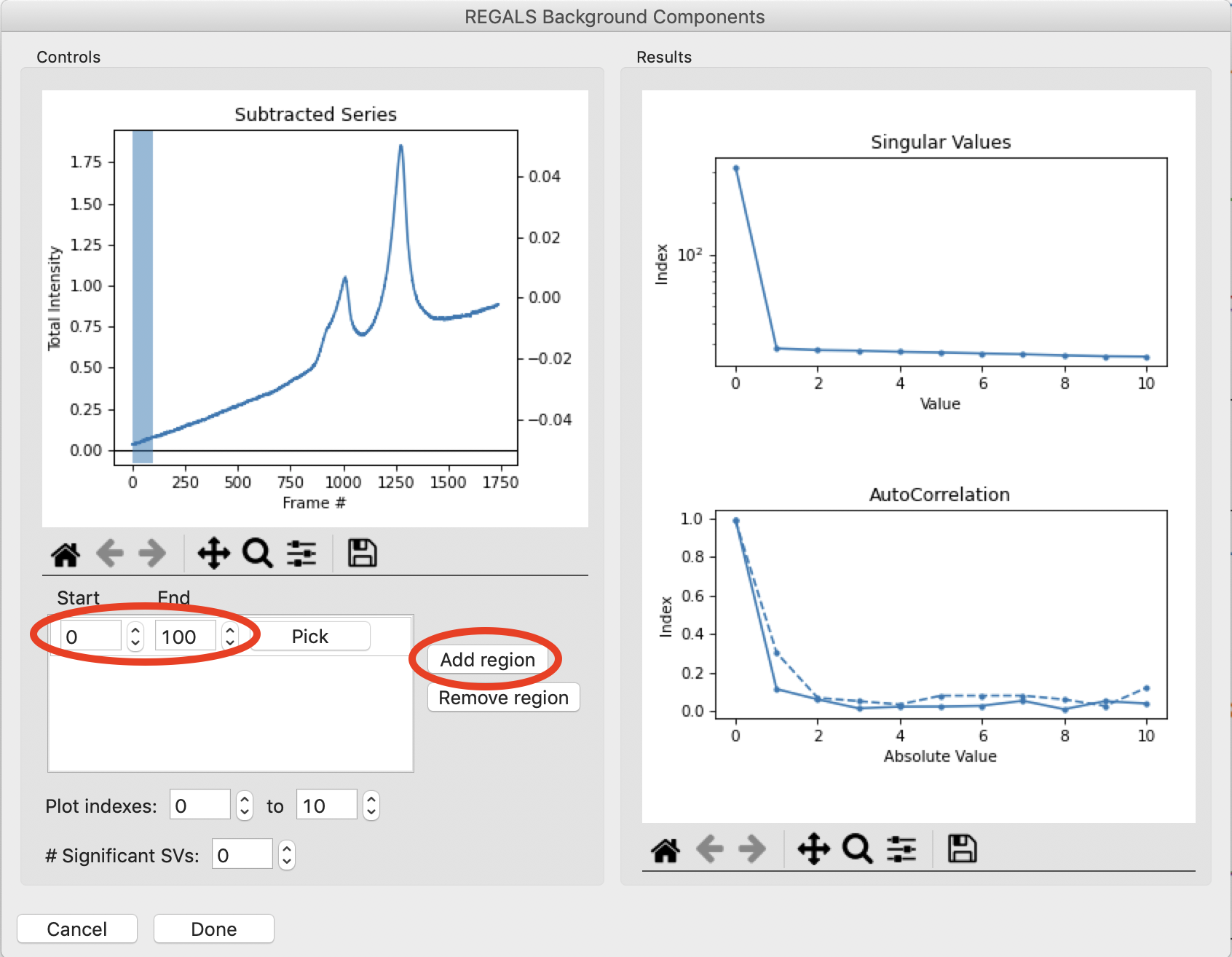
In the Background Components window, click “Add Region” to add a region to the plot. The SVD of the data in that region is shown in the plots on the right. Set the range of that region to 0 to 100. The SVD plots show that there is only one strong component in the dataset in this range.
Add a region corresponding to the last 100 frames of the dataset. This will appear as a second colored range on the series plot, with corresponding second colored sets of lines in the SVD plots on the right. Notice that there is just one component in the last 100 frames of the dataset.
Note: The left autocorrelation is shown with the solid line, the right autocorrelation with the dashed line.
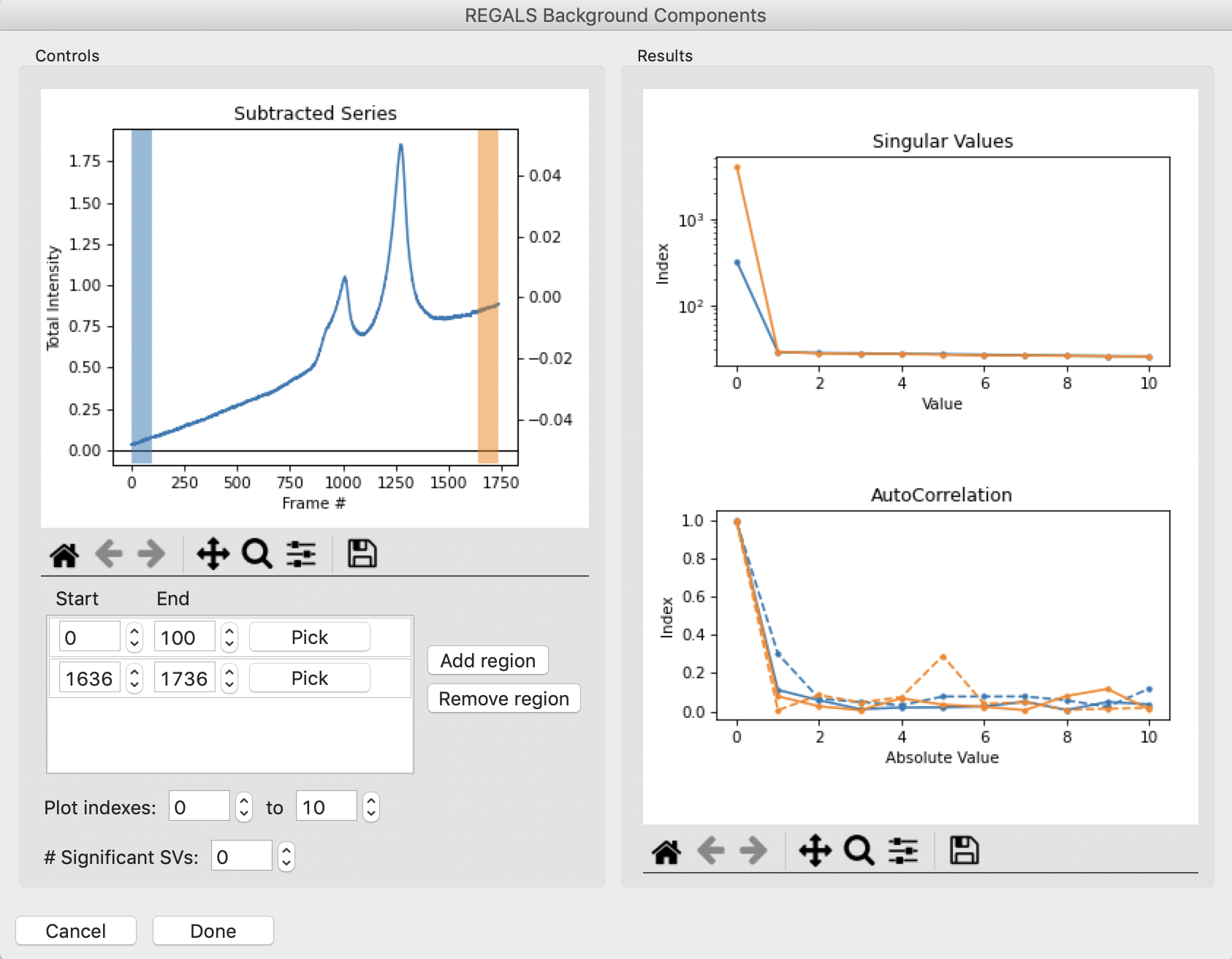
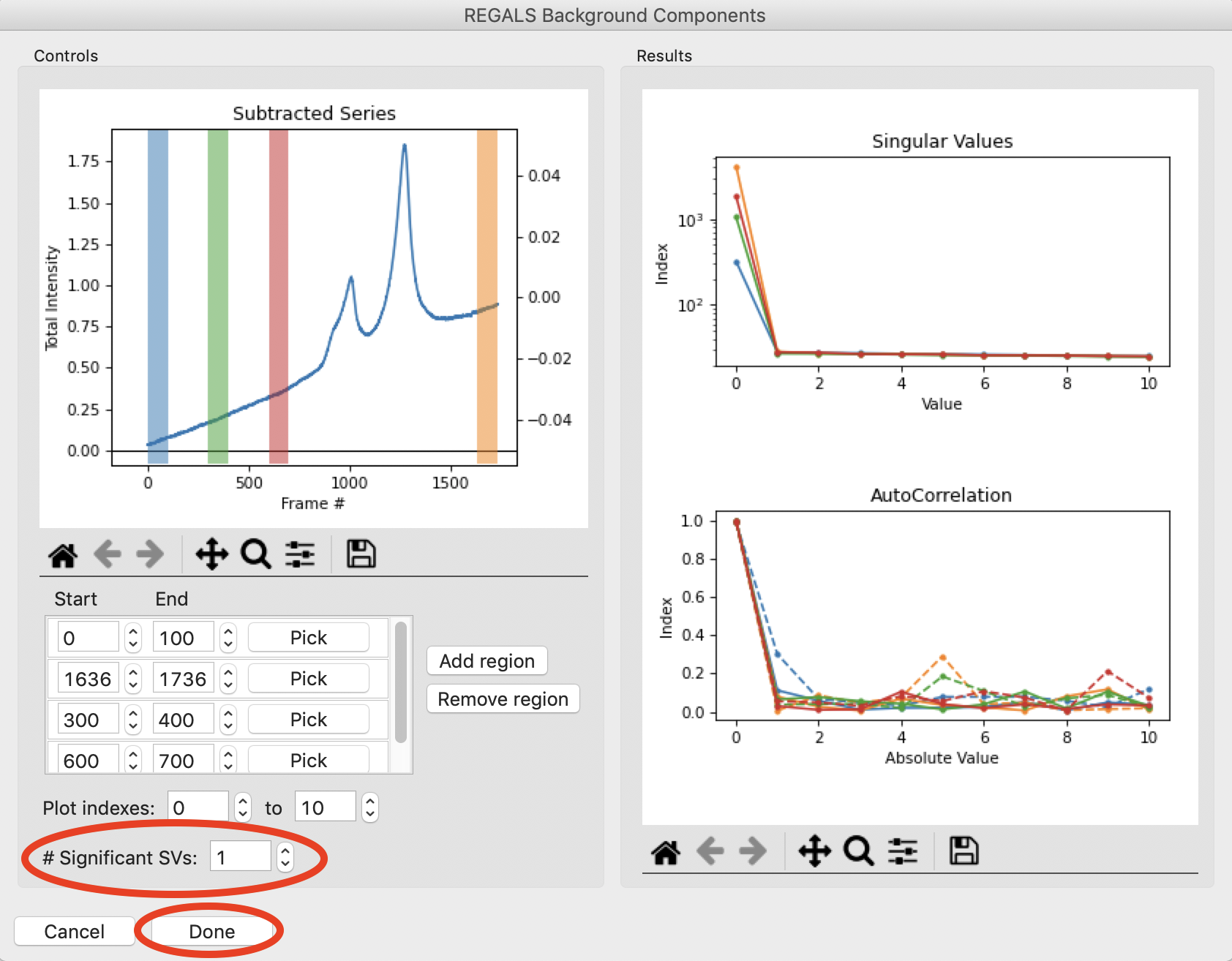
Add several more similar regions through the initial upward sloping buffer region. Notice that there appears to be just one strong value throughout most of the buffer region, both before and after the eluted peaks. So as a starting point we will set the number of significant background components to 1, by setting the “# Significant SVs” input to 1. Once that’s done, click the “Done” button.
Tip: You can remove regions if they are not longer useful. To do so, select the region by clicking to the right of the pick button and then clicking the “Remove region” button.
The Background Components window will close and the number of background components shown in the main REGALS window will update. The main REGALS window will now be fully visible.
Note: You can reopen the Background Components window using the “Find background components” button if desired.
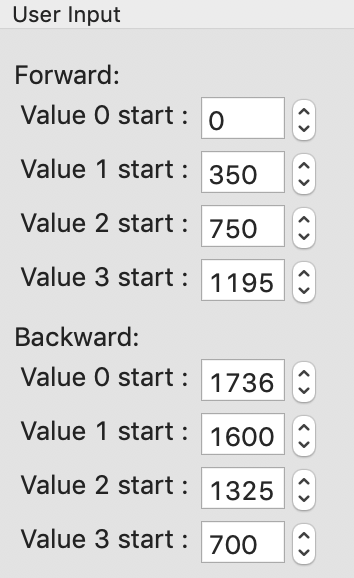
In the User Input panel, tweak the “Forward” value start frames so that the frame number, as indicated by the open circle on the plot, aligns with where the singular value first starts to rise above the baseline. This should be around 0, 350, 750, and 1195.
Note: For the Forward EFA plot, SVD is run on just the first two frames, then the first three, and so on, until all frames in the range are included. As more frames are added, the singular values change, as shown on the plot. When a singular value starts rising above the baseline, it indicates that there is a new scattering component in the scattering profile measured at that point. So, for the first ~350 frames, there is only one scattering components (i.e. just buffer scattering). At frame ~350, we see the second singular value (the singular value with index 1, labeled SV 1 on the plot) start to increase, showing that we have gained a scattering component.
Note: One component starts above baseline, indicating there is already a significant scattering component at the start of our dataset. In this case that is the sloping buffer gradient.
In the User Input panel, tweak the “Backward” value start frames so that the frame number, as indicated by the open circle on the plot, aligns with where the singular value drops back to near the baseline. This should be around 700, 1325, 1600, and 1736.
Note: For the Backward EFA plot, SVD is run on just the last two frames, then the last three, and so on, until all frames in the range are included. As more frames are added, the singular values change, as shown on the plot. When a singular value drops back to baseline, it indicates that a scattering component is leaving the dataset at that point.
Note: One component ends above baseline, indicating there is still a significant scattering component at the end of our dataset. In this case that is the sloping buffer gradient.
Click the “Next” button in the bottom right corner to move to the last stage of the REGALS analysis.
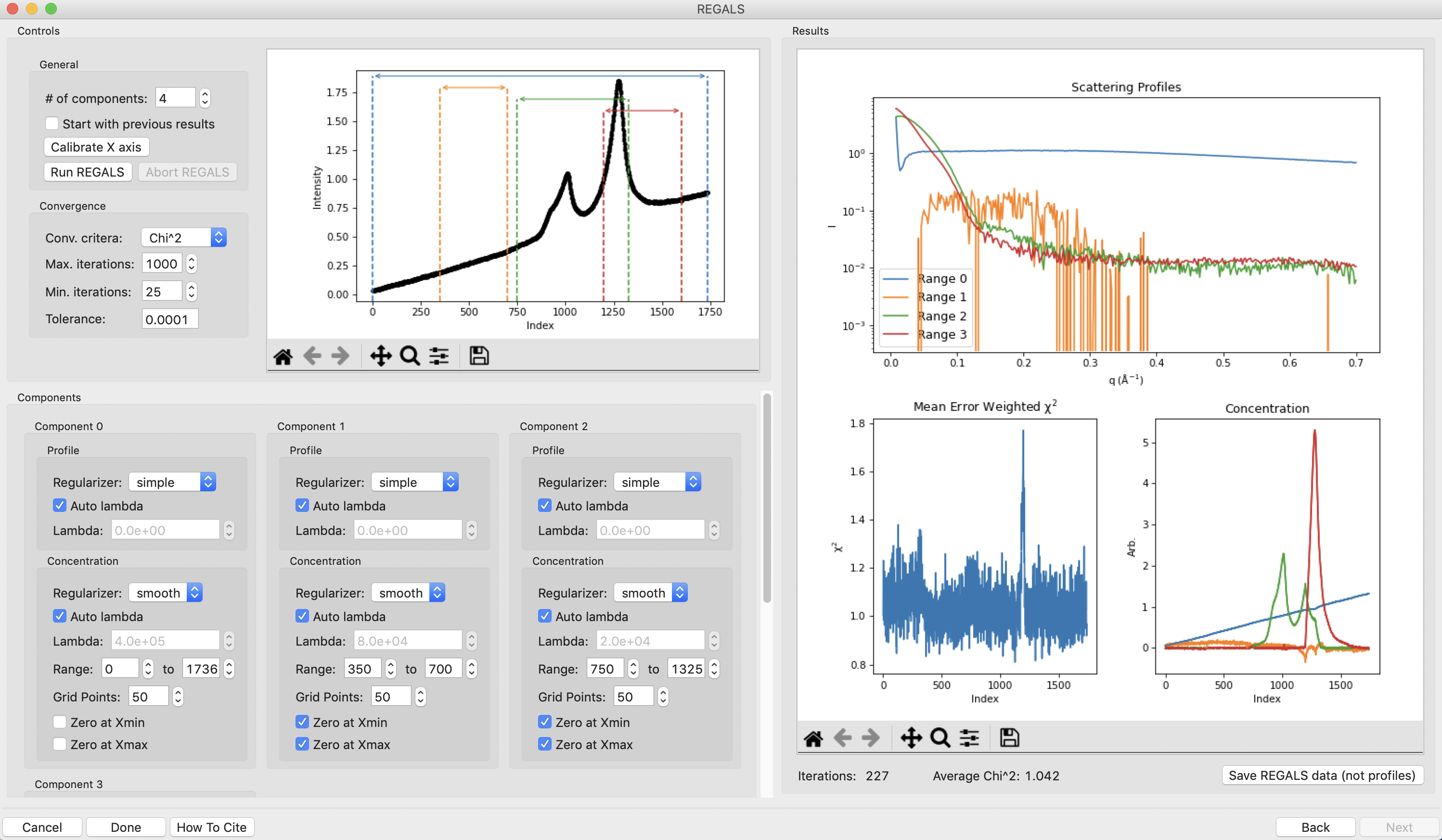
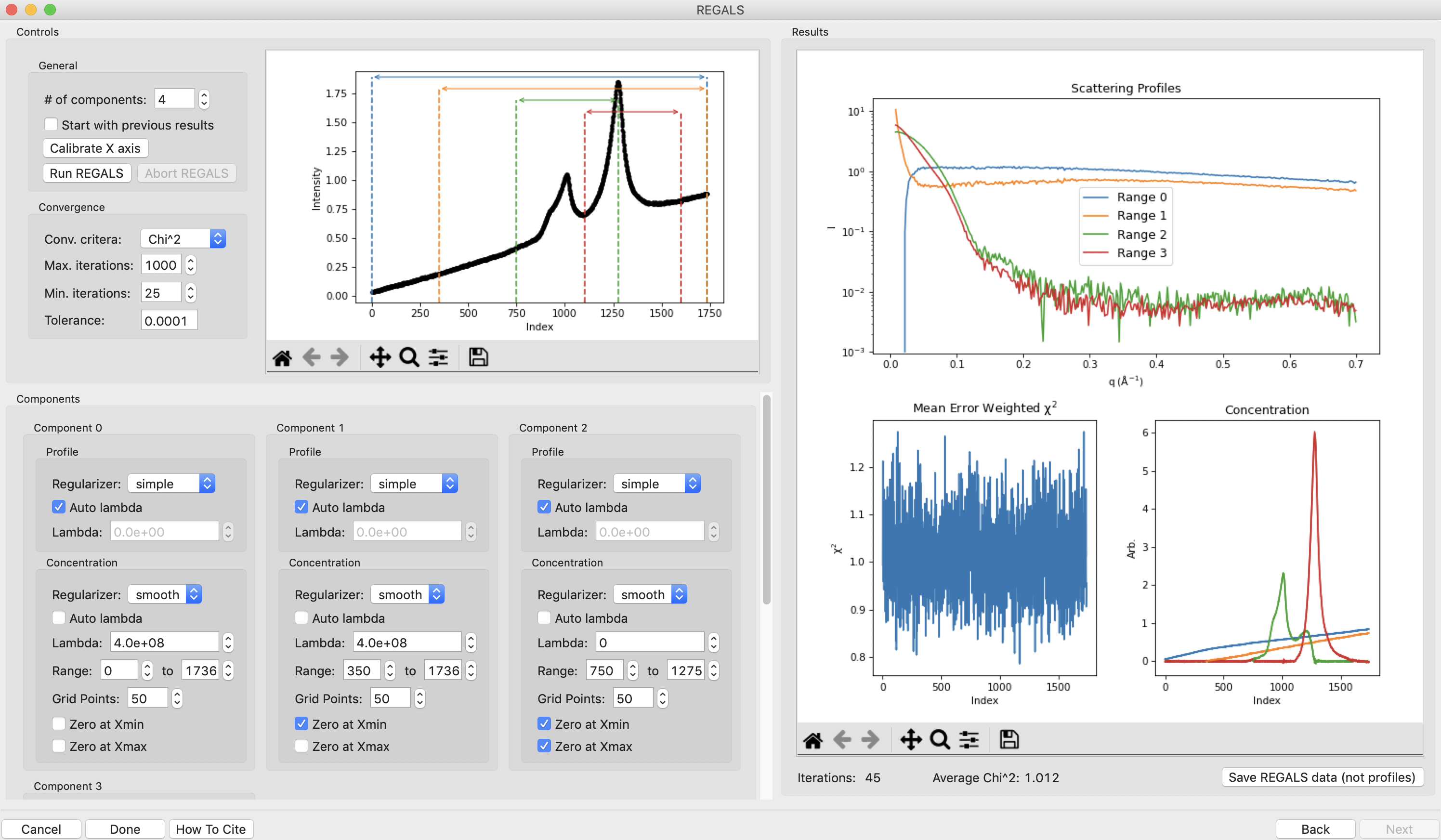
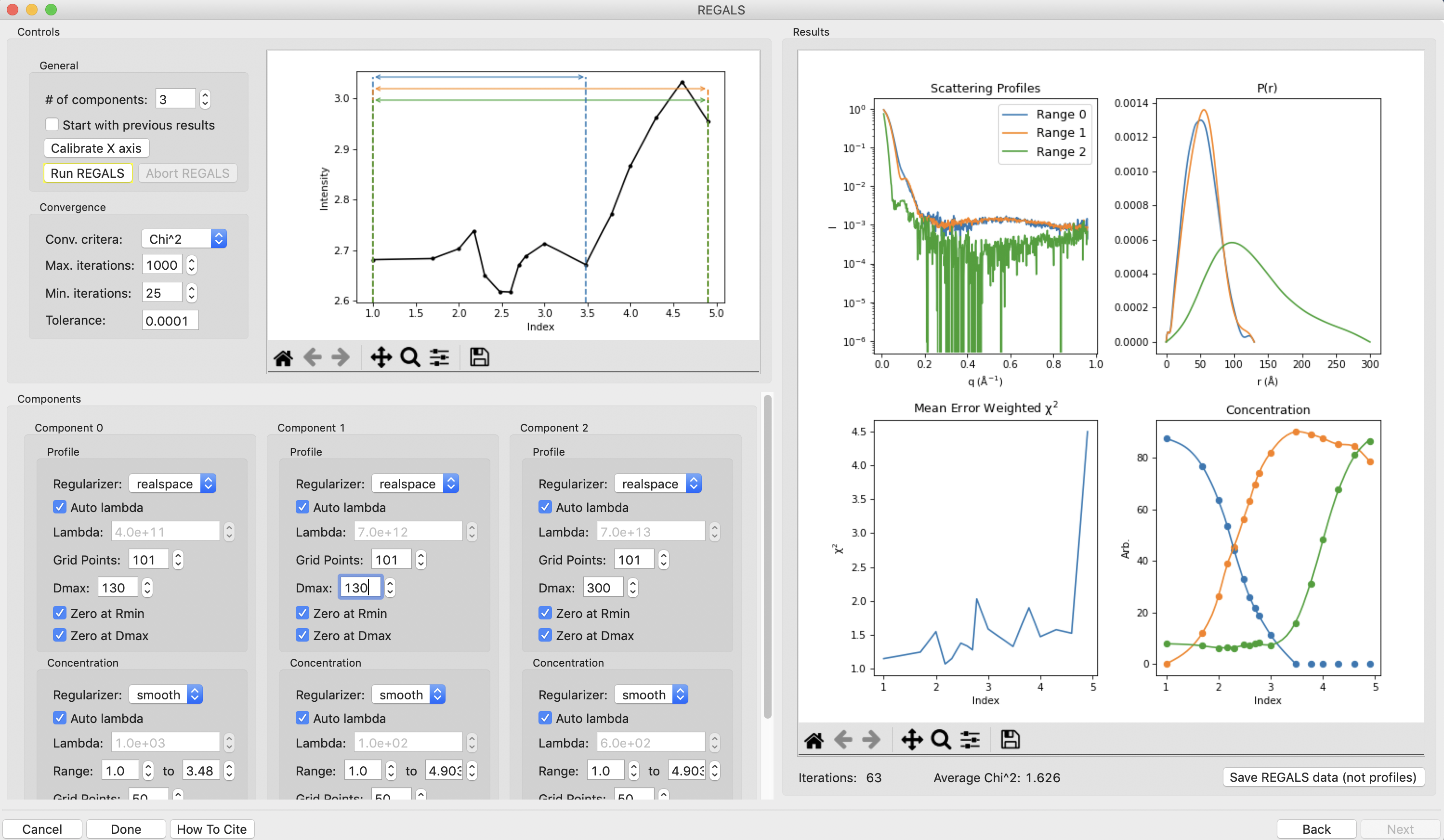
This window shows controls on the left and results on the right. In the controls area at the top are general controls. You can adjust the number of components, calibrate the X axis, and set the convergence criteria for the REGALS algorithm. A plot of the ranges is also shown. On the bottom are the controls for each individual component. We won’t go through all the possible permutations for each setting, so if you want to know more check out the links at the top of this tutorial.
Note: The ranges are automatically assigned based on the start and end points for components found in the EFA plots. Background components ranges are assigned on the principle of first-in last-out, whereas all the other component ranges are assigned by first-in first-out.
Note: Components are only shown three across. Scroll down in the component area to see more component settings.
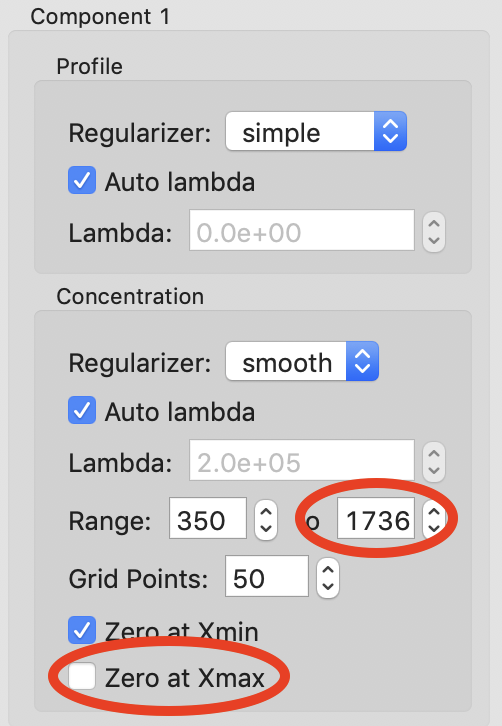
Now we need to start refining our component ranges, and tweaking other settings in the components. Component 0 looks good for now, so we will start with component 1. On the concentration plot on the right, notice that despite the component 1 range being defined from only 350-700, the component shows features at a wide range of frame numbers (index). Looking at the scattergram with the ranges plotted, there’s no obvious elution component in the range where component 1 is defined. This means that component 1 is likely a background component as well. Since the SVD for the background components and the EFA plots were not clear on where the component should end, we will fit it from the start point we found, 350, until the end of the dataset. To do this, change the endpoint of the concentration range to 1736. Also uncheck the ‘Zero at Xmax’ box for this component, as it may contribute to the buffer scattering at the end of the dataset.
Tip: If you return to the Background Components window, if you add a single range from 0 to 700 you’ll see two components, indicating that there are likely multiple background components. However, if you look at the end region, assuming you avoid the tail of the peak (~1600-1736) there’s only one component. So it’s not clear where the first component might end and the second one start, and how much coexistence there is between these two background components. In this case, fitting both to end at the end of the dataset works well.
Because it can take a while to run, REGALS does not automatically update the results. To see how changing the range changed the deconvolution, click the “Run REGALS” button.
Note: If lambda is automatically updated for a component, this value in the GUI will not be updated until you run REGALS.
Note: When you have changes to your deconvolution settings and REGALS hasn’t been run with those settings the “Run REGALS” button will have a yellow background.
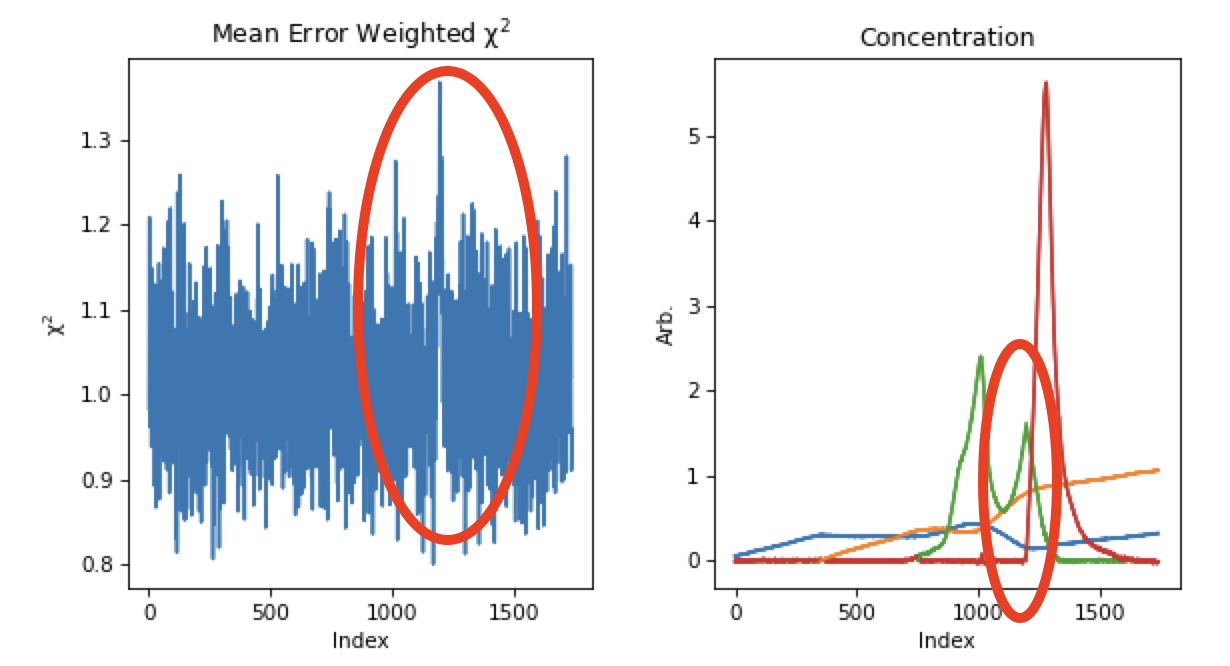
There is a definite improvement in the REGALS results after rerunning the data. Next we will refine the protein components. We will first refine the ranges. On the concentration plot, notice that the component 3 (red) concentration is pulled down to zero pretty sharply on the left side. At the same point there’s a peak in the component 2 (green) concentration right where the red one starts. There’s also a small spike in the chi^2 plot around frame 1200, which is where component 3 starts. This indicates that we’ve restricted component 3 excessively and some of the scattering is going into component 2. We will change the range for component 3 to start at an earlier point and see how that affects the deconvolution. To do this, set the start of component 3 to 1150 and run REGALS.
After running REGALS, notice that the chi^2 spike is completely gone, and that the range 3 concentration is coming back down to zero in a more natural way. Also notice that the spike in component 2 concentration is reduced. If you look closely at the component 2 concentration you can see a bit of a double peak around ~1150. There could be a little bit more component 3 there, so we will start the component 3 range earlier. Try 1125 and 1100 for the component 3 start.
As there’s minimal change between 1100 and 1125, set the component 3 start back to 1125.
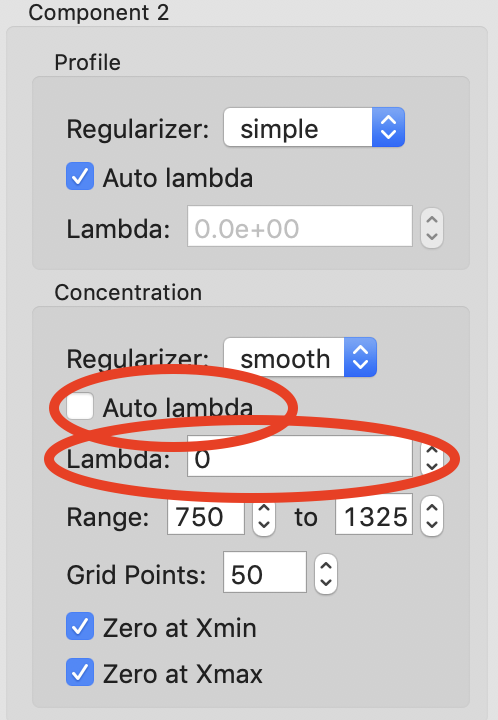
At this point the deconvolution is starting to look reasonable. There’s nothing obviously wrong with the component ranges, so next we will adjust the lambda values for the components. These control the degree of smoothing in the deconvolution. For strong components with lots of measured profiles, like the peaks in this dataset, we don’t need a large lambda. In fact, we might not need any lambda. For component 2 and 3 concentrations turn off “Auto lambda”, and set the lambda value to 0. Then run REGALS again.
Tip: Make sure you’re setting lambda for the concentration, not the profile, for each component.
After running REGALS with the peak component concentration lambdas set to 0, the component 2 concentration (green) has a small negative dip at the end of the concentration range. This indicates that we should adjust the range for that component. In particular, we’ll reduce the end point to try to eliminate that dip. Try 1300 and 1275 as endpoints for component 2 concentration.
Note: If we had set the lambdas particularly poorly, we would start to see the chi^2 plot deviate from ~1. Since we don’t, we can conclude that our lambda values are probably okay.
Notice that 1275 essentially eliminates the dip in the concentration. Set that as the endpoint for the component 2 concentration.
Try: You can try small tweaks near 1275 if you like, but you shouldn’t see significant changes in the concentration shape. So we’ll leave it set at 1275 for now.
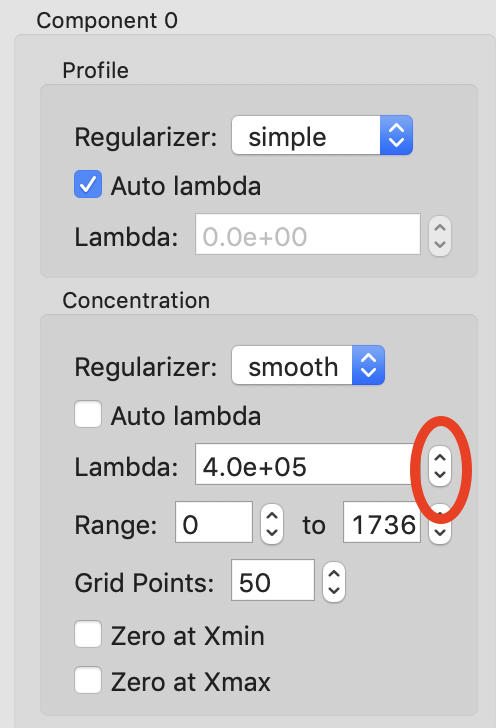
The final thing we will adjust is the lambdas for the background component concentrations. Those concentration profiles are a bit wavy. We would expect the concentrations of the buffer to increase linearly, since a linear salt gradient was applied during elution. To increase the smoothness of the concentration, we will increase lambda. Turn off “Auto lambda” for components 0 and 1. Then use the up arrow next to the lambda box to increase each lambda by an order of magnitude. Run REGALS to see how this affects the deconvolution.
Note: Generally you want to adjust lambda by an order of magnitude or more. Smaller adjustments will have minimal effect on the deconvolution.
Tip: You can also type a new lambda value directly into the box.
There are two major changes with the new lambdas. First, the high q of the scattering profiles for ranges 2 and 3 will get more similar. Second, the concentration for ranges 0 and 1 will get smoother. The change in high q comes from a decrease in the high q values component 2, while component 3 stays mostly the same. This implies that more of the buffer scattering is getting picked out component 2. Keep increasing both buffer component lambdas by an order of magnitude until this stops changing. You will also see a sudden and dramatic change in the component 1 profile at some point.
Once you see the high q backgrounds match and the large change in the scattering profile for component 1, it means you’re oversmoothing the buffer components. Reduce the lambda for both buffer components to the last good value, which would be ~4e8.
This is a more or less optimum solution for REGALS deconvolution for this dataset. Since we’re satisfied, we can now save the results. First, click on the “Save REGALS data (not profiles)” button in the bottom right corner and save. This saves a spreadsheet (.csv) file with all of the information from REGALS that isn’t the scattering profiles, including the component settings and concentration and chi^2 vs. frame data.
Finally, click the “Done” button to close the REGALS window and send the deconvolved scattering profiles to the Profiles Plot.
In the main RAW window, go to the Profiles control tab and the Profiles plot. There you should see the deconvolved profiles. The labels _0, _1, _2, and _3 correspond to the 0, 1, 2, and 3 components from REGALS.
Deconvolving equilibrium titration series SAXS data
Titration series SAXS data looks at the change in scattering profile of a macromolecule as a substance (salt, substrate, another macromolecule, etc.) is titrated in or our of the solution. It is done in equilibrium, so buffers are prepared ahead of time and samples are equilibrated in the buffer, then measured. These measurements are typically done in batch mode SAXS (without in-line separation from SEC), and often involve transitions between different conformations or oligomeric states, and so the measured scattering at a given titration point is not from a homogeneous and monodisperse sample. We can use REGALS to deconvolve the different scattering components in the titration series to get pure profiles for each component.
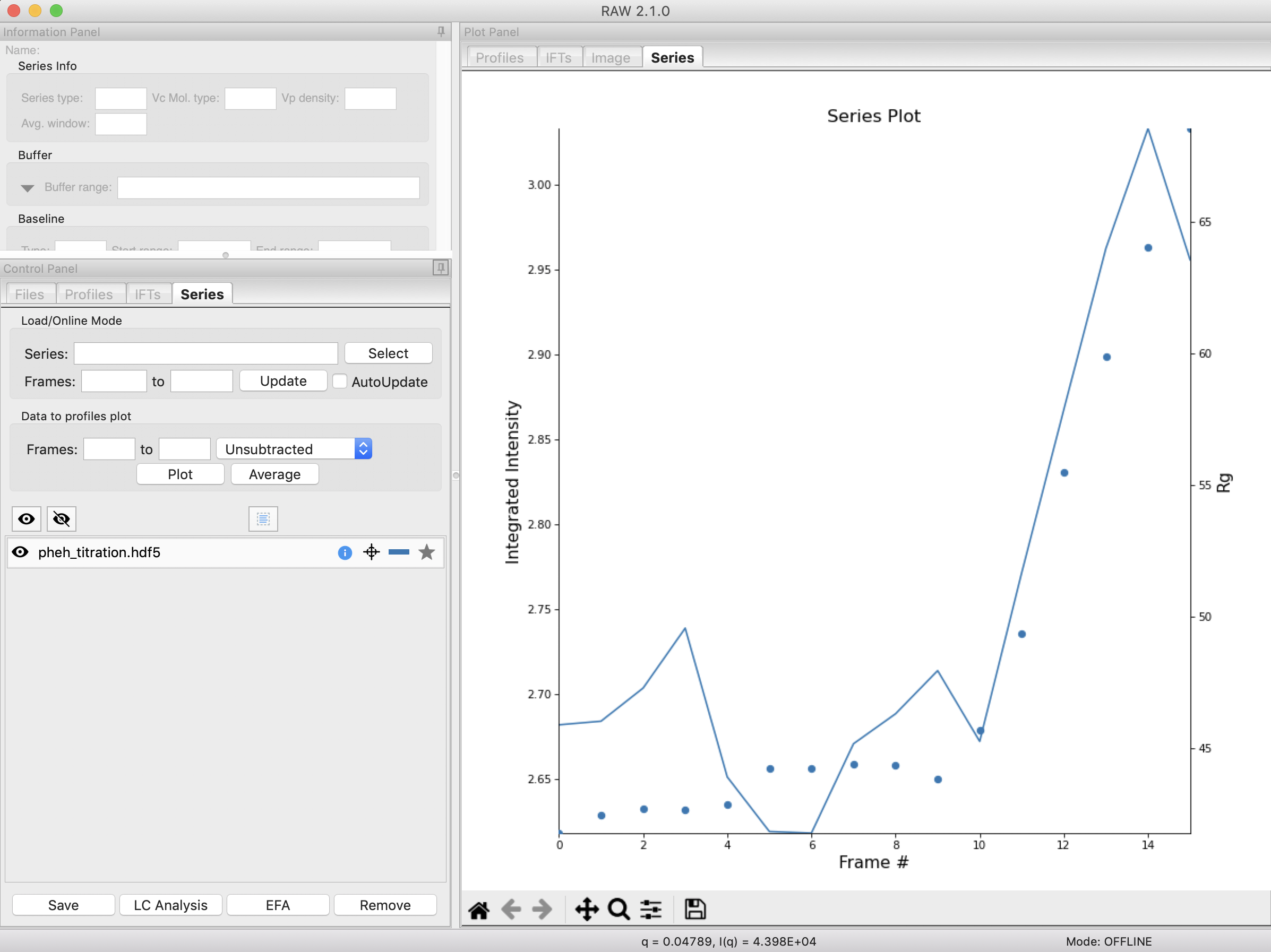
Clear all of the data in RAW. Load the pheh_titration.hdf5 file in the series_data folder.
Note: This data are a titration series of phenylalanine (L-phe) into a sample of phenylalanine hydroxylase (PheH). 16 different concentration points were collected, ranging from 0 to 80 mM L-phe. The data are already background subtracted, using buffers containing a matching concentration of L-phe. A conformational change has previously been observed on PheH binding L-phe. A small amount of aggregation was also observed at all concentrations, preventing the use of saturated endpoints in the titration series to completely determine each conformational state in batch mode experiments. We will deconvolve both conformations and the aggregate scattering from the titration series. Prior analysis of this data without the use of REGALS is published.
Note: The data were provided by the Ando group at Cornell University, and were originally published in the paper: Meisburger, S. P. et al. (2016). Domain Movements upon Activation of Phenylalanine Hydroxylase Characterized by Crystallography and Chromatography-Coupled Small-Angle X-ray Scattering. J Am Chem Soc 138, 6506–6516. DOI: 10.1021/jacs.6b01563. It is also available from the REGALS github repository.
We will use REGALS to extract out the scattering of the individual conformers and the aggregate in the titration series. Right click on the pheh_titration.hdf5 item in the Series list. Select the “REGALS” option.
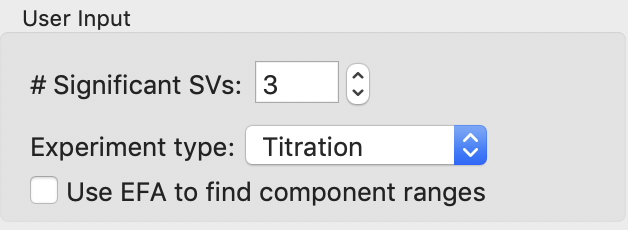
Normally we use the plots of singular values and autocorrelations to determine the number of significant singular values (i.e. scattering components) in the dataset. Based on the plots of this titration series, there are ~4-5 significant singular values (SVs), for reference RAW’s automated method found 4 such values. However, prior knowledge indicates there are only two conformations we care about, and we suspect the other components are various aggregates. So we will fit the data to three components: each conformation and a single aggregate scattering component. Set the “# Significant SVs” to 3.
Set the experiment type to “Titration”. This affects the default settings later in the deconvolution.
Because we have so few data points, and we’re using fewer components than the actual number of significant SVs, trying to find the component ranges using the EFA plots will not be useful. Uncheck the “Use EFA to find component ranges” box.
Click the “Next” button in the lower right-hand corner of the window to advance to the final stage of the REGALS analysis.
Note: In this case, since we aren’t determining the component ranges with EFA, REGALS is not automatically run initially. We will have to set the component settings, then run REGALS.
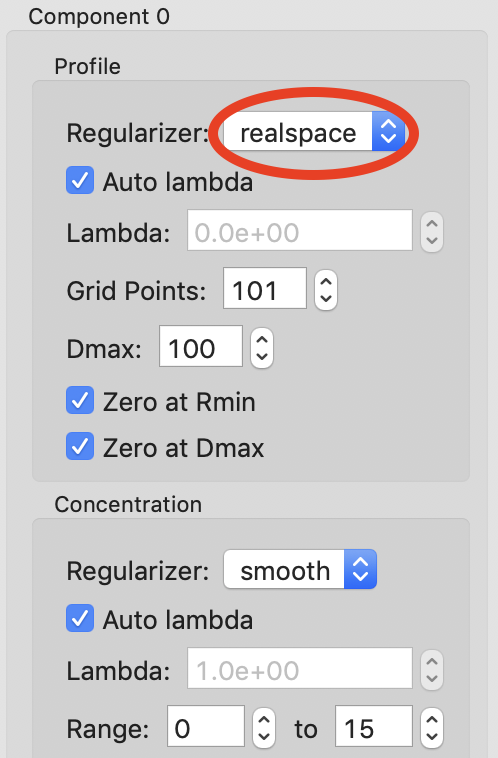
Notice that the profile part of each component has a “realspace” regularizer. This means that instead of constraining the data in q space via the scattering profile we will be constraining the data in real space using the P(r) function. So in addition to setting component ranges for the concentration and the lambda values, we will also set the Dmax value for the P(r) function.
The titration concentrations are not equally spaced from 0 to 80 mM, so we will calibrate the X axis appropriately. Click the “Calibrate X axis” button.
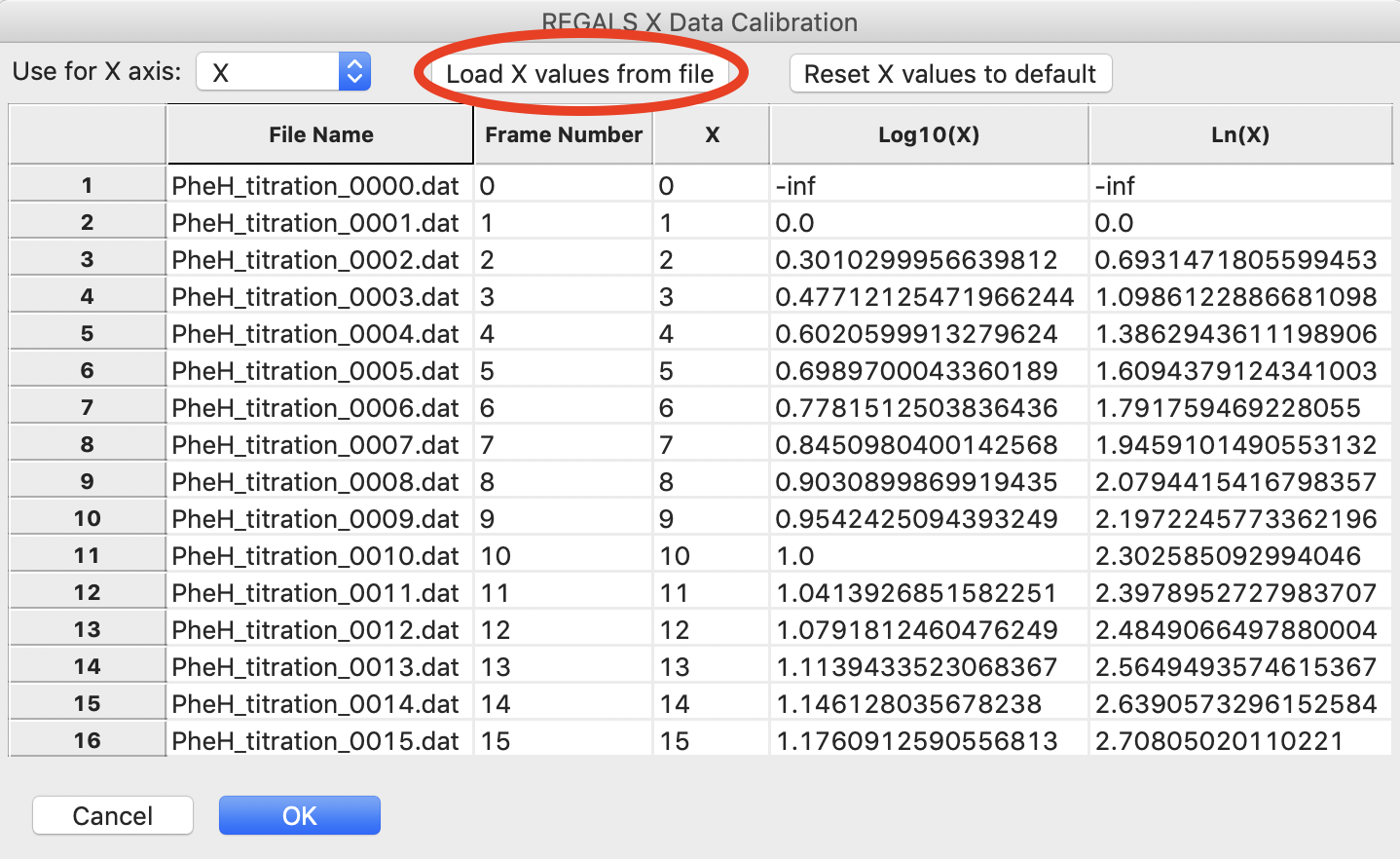
In the window that opens click the “Load X values from file” button.
Select the pheh_titration_conc.txt file in the series_data folder and load it in.
Note: A calibration file should consist of a single column of the concentration values, in the order that the profiles were loaded into the series. So the first line of the file has the concentration for the first profile in the series, and so on.
Upon loading you should see the values in the X column update.
Note: The concentrations are in uM, so you will see concentrations from 0 to 80000.
The concentration values are not linearly spaced, as is typical of a titration series. It is also most common to work with titration series on a logarithmic concentration scale. To do this, we need to define the first concentration as not zero (as log(0) is undefined). For this data we will set the concentration to 10 uM. Double click in the first box in the X column and enter 10.0.
Note: You can enter all the concentrations manually if you want, you don’t have to create the concentration file we loaded in the previous steps. However, for a long series this can get a bit tedious.
As we want to work with our data in log space, select “Log10(X)” in the “Use for X axis” list. Then click the OK button to exit the window and save the X calibration.
In the main REGALS window, notice that the X axis is now calibrated as Log(concentration), and that the ranges for the concentration components have updated accordingly.
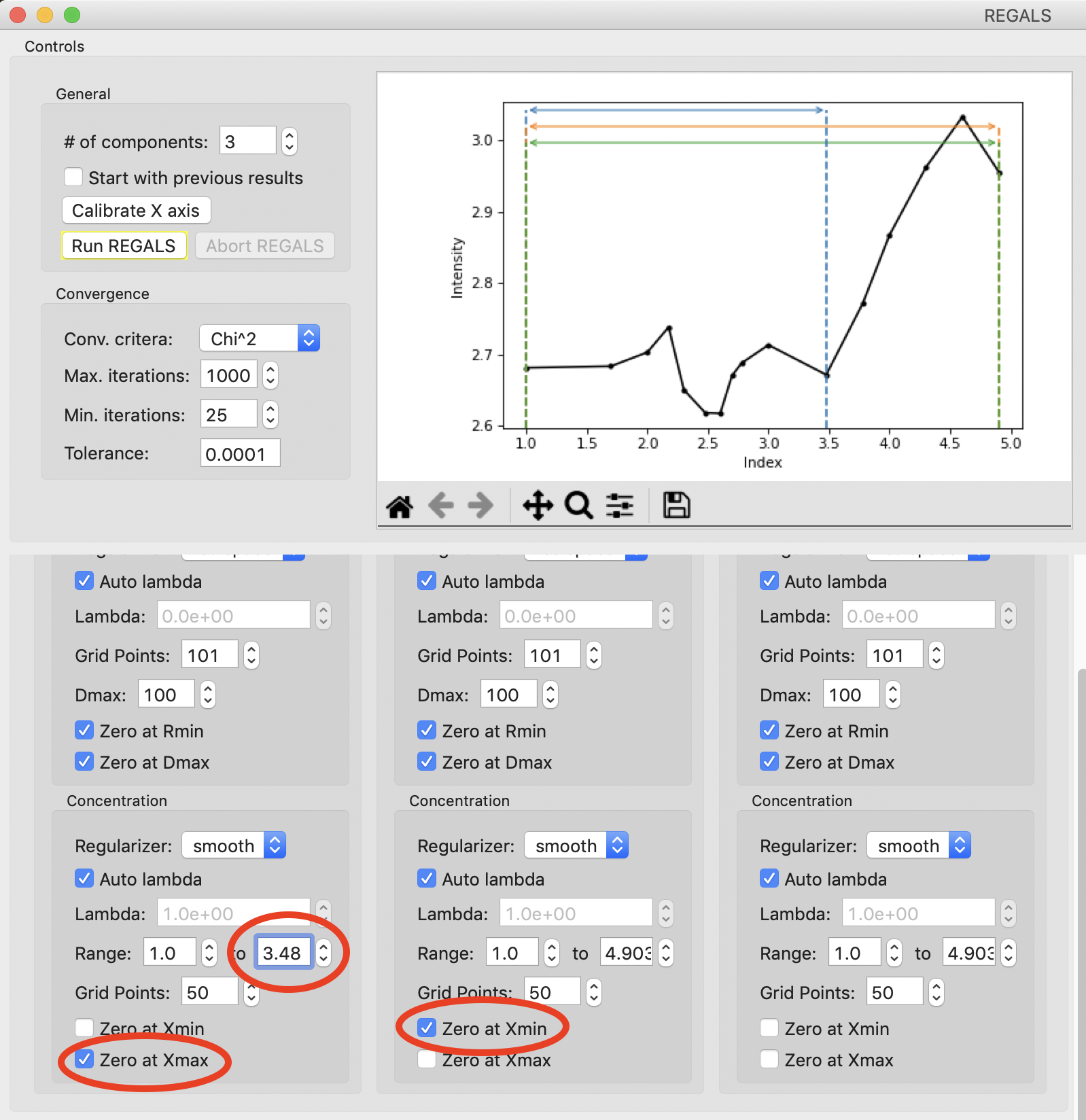
Next we will set the ranges for our components. We will use components 0 and 1 as the different conformations, resting and active respectively, and component 2 as the aggregate. Prior analysis of the system showed that of the two conformations, only the resting conformation, component 0 is present at 0 mM L-phe. So set the “Zero at Xmin” to True for component 1.
Prior analysis showed that features of the scattering profile associated with the active state saturated above 3 mM. So we will assume that there is no contribution to the scattering from the resting state at/above 3 mM (3.48 on the log10(X) axis). Set the end range for component 0 to 3.48, and apply a Zero at Xmax boundary condition to it.
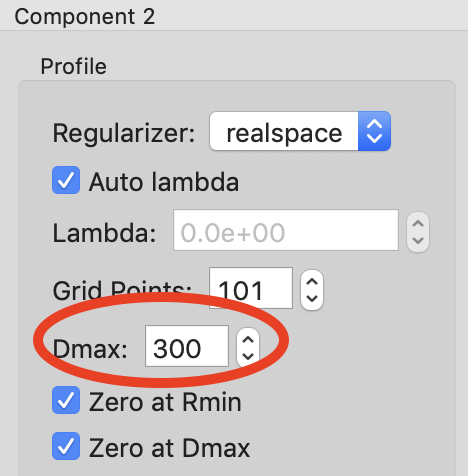
We will apply not constraints to the concentration range of the aggregate, so we are done with the concentration ranges. Next we need to set the Dmax values for the components. We’ll start with the aggregate. Since we have no prior knowledge about the aggregate, we will assume it is a non-specific size. Because of the q range of the data, the largest dimension of an object that can be measured is ~300 Å, based on the Shannon limit of \(D_{max}<\pi/q_{min}\). So we will set the Dmax value for the aggregate, component 2, to 300.
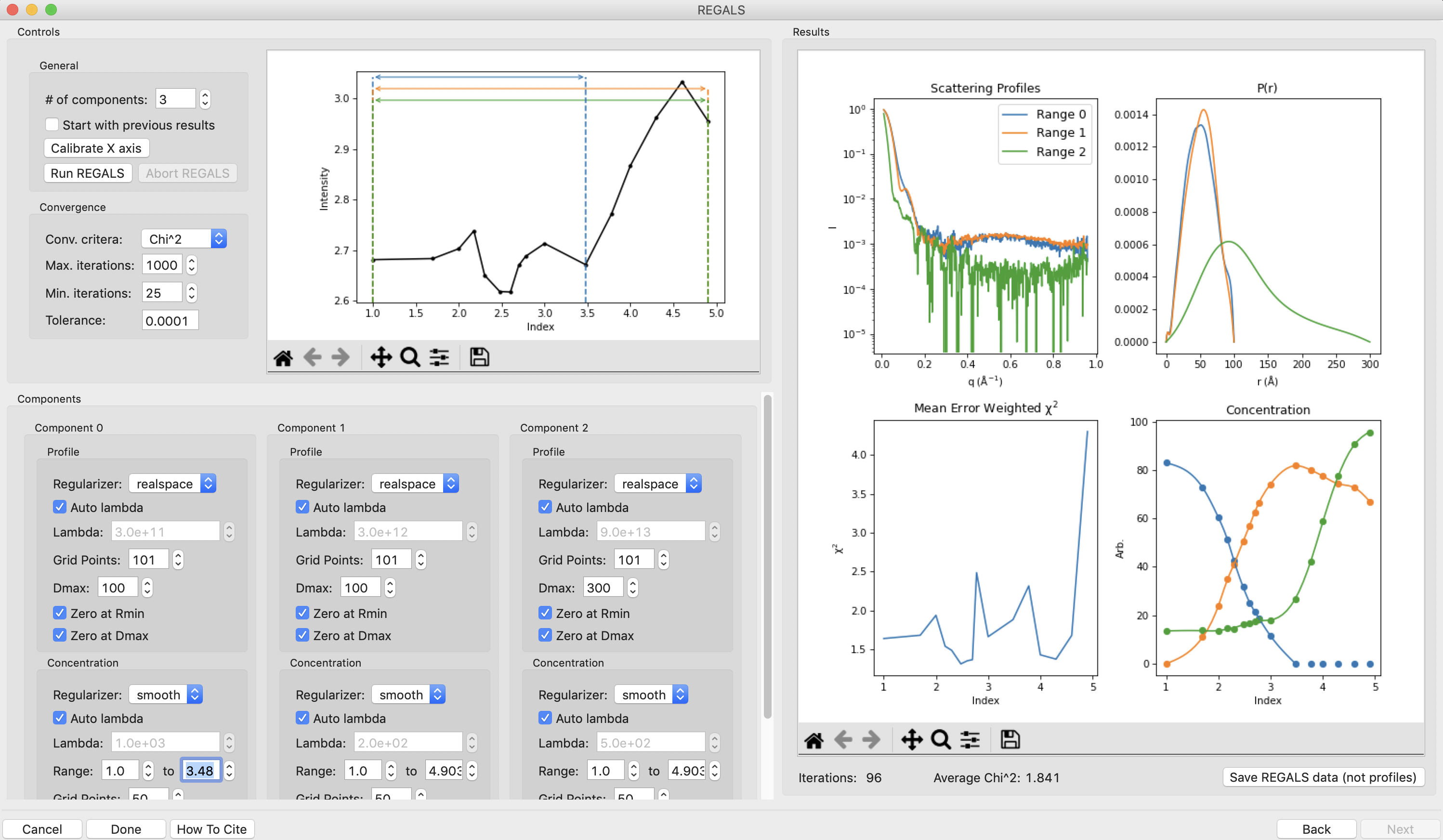
We will now run REGALS to get an initial look at the deconvolution. Click the “Run REGALS” button.
Looking at the results, it’s already a reasonable deconvolution. The concentrations make sense with previous knowledge, e.g. that there’s a transition from the resting (component 0) to active (component 1) with increasing L-phe concentration, and that there’s a low level of aggregate throughout that increases significantly at higher concentrations of L-phe. The profiles and P(r) functions, while not completely correct, are at least reasonable shapes, and the chi^2 is mostly relatively low.
Note: On the concentration plot, the markers are the concentrations calculated at the titration points. The smooth lines are the concentration calculated at the regularlizer grid points, so it is effectively interpolated between the measured titration points. When you have more than 40 profiles in the series, only the concentration at the actual measured points is shown, and there it is shown as a continuous line, not individual points (as in the above IEC-SAXS example).
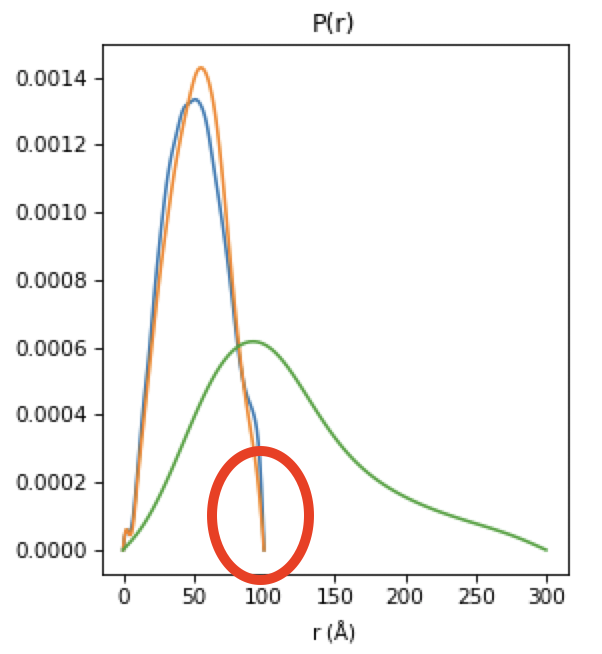
Next we will refine the Dmax values for the resting and active states. On the P(r) plot, notice that for both components the P(r) function is forced to zero sharply, indicating that an underestimated Dmax value. Increase both Dmax values to 110 and run REGALS again.
Notice that at a Dmax of 110 the P(r) functions are still somewhat forced to zero, but the chi^2 is lower, so this has improved the deconvolution. Continue increasing Dmax in steps of 10-20 until you reach 160. You should notice several things. First, there’s a range from ~130-150 where the chi^2 is relatively stable, indicating Dmax values in those ranges all provide relatively good fits to the data. Second, as you increase Dmax the concentration of the aggregate decreases, particularly in the lower titration concentrations. This implies that having a larger Dmax is letting that component take up some of the aggregate scattering. Third, after ~120 the P(r) functions stop looking as forced to zero. Fourth at 160 the chi^2 starts noticeably increasing, indicating that’s too large for the Dmax value. Based on this, we want to pick a Dmax value near 130, to exclude as much of the aggregate as we can while still getting good P(r) functions and chi^2 values.
Set the Dmax of both components to 130 and run REGALS.
Note: The Dmax values found by previous analysis was ~130, so this validates our choice of Dmax.
Note: The Dmax values for different components won’t necessarily agree. In this case they happen to.
Tip: If it takes a while to run REGALS every time you change a component, you can speed up the convergence by starting with the previous results. To do so, you would check the “Start with previous results” box. Then change the convergence criteria to “Iterations” and set the number of iterations to 10. This will allow you to quickly iterate on changes like Dmax, as long as the magnitude of the change is relatively small. Just be sure to set the convergence criteria back to the default (not using previous results, and Chi^2 with 1000 iterations) to do your final REGALS run.
The REGALS deconvolution is now as optimized as we can make it. Notice that there’s still a relatively high chi^2 value for the last frame. This indicates that the aggregate may be changing shape as the amount increases, and so a single component cannot fit all the data well. You can redo the deconvolution without the last data point if you want, the results are very similar albeit without the chi^2 spike for the last point. Since we’re satisfied with these results we can now save them. First, click on “Save REGALS data (not profile)” and save.
Note: Among other things, this .csv file contains the P(r) functions, and the smoothed concentration curves (lines on the concentration plot). In this case the smoothed concentration curves are particularly useful because the protein changes shape but not size. As the P(r) functions are normalized to I(0), the concentration curves for both components are on the same overall scale. This means they differ by simply a uniform scale factor from the true concentrations (e.g. in mg/ml), and so could be useful to help characterize the two state transition. This will not always be true, such as if you’re characterizing an oligomerization reaction.
Finally, click the “Done” button to close the REGALS window and send the deconvolved scattering profiles to the profiles plot.
General notes
It is okay to mix and match different types of regularizers (e.g. have both smooth and real space profile regularizers) for the same series.
You can change the regularizers away from the defaults for a given experiment type.
The REGALS examples shown here were chosen to demonstrate the features of the GUI. REGALS is not restricted in application to just IEC-SAXS and titration data. It has been successfully applied to time resolved SAXS data (similar to the titration series example), and we expect it will be applied to a range of other types of experiments as well.
As you saw in the PheH titration series example, it is quite useful, and sometimes necessary, to have additional information to input to the deconvolution, such as the range of the components, or a known maximum dimension. One of the advantages of REGALS is that it can incorporate these additional pieces of information to improve the deconvolution.
By default, RAW bins the profiles before doing an SVD and calculating the evolving factor plots, in order to speed up the process. The final REGALS rotation is done on the full unbinned dataset. You can turn binning on and off and adjust the binning parameters in the Series options panel in the Advanced Options window.